Упр.4.367 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
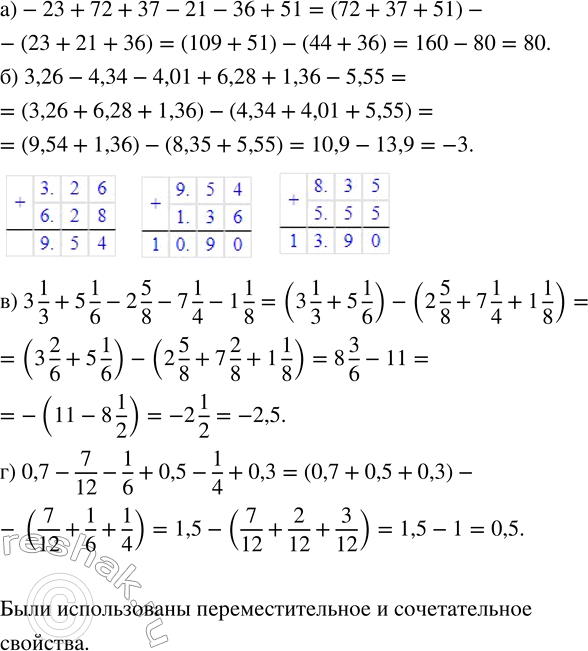
Решение #2 (Учебник 2023)

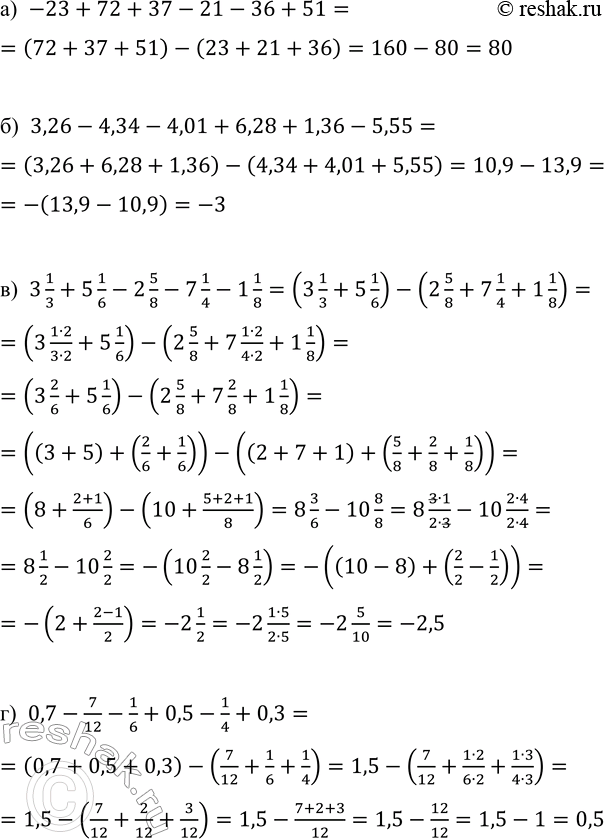
Решение #3 (Учебник 2023)
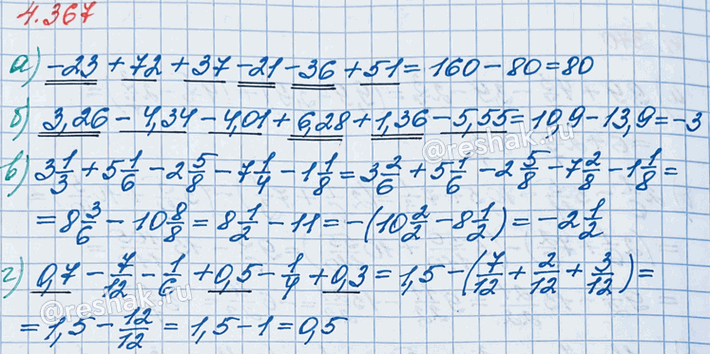
Решение #4 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Вычислите значение алгебраической суммы:
а) -23 + 72 + 37 - 21 - 36 + 51;
б) 3,26 - 4,34 - 4,01 + 6,28 + 1,36 - 5,55;
в) 3 1/3 + 5 1/6 - 2 5/8 - 7 1/4 - 1 1/8;
г) 0,7 - 7/12 - 1/6 + 0,5 - 1/4 + 0,3.
Какие свойства рациональных чисел вы использовали?
Вычислите значение выражения рациональным способом (сложив отдельно положительные и отдельно отрицательные числа):
а) -23 + 72 + 37 - 21 - 36 + 51;
б) 3,26 - 4,34 - 4,01 + 6,28 + 1,36 - 5,55;
в) 3 1/3 + 5 1/6 - 2 5/8 - 7 1/4 - 1 1/8;
г) 0,7 - 7/12 - 1/6 + 0,5 - 1/4 + 0,3.
При выполнении вычислений сумму отрицательных чисел записываем в одну скобку, а сумму положительных чисел в другую скобку, затем выполняем вычисления в скобках и складываем полученные результаты, опираясь на следующие правила:
- для того, чтобы сложить два числа с разными знаками, необходимо найти модули слагаемых и из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем.
- для того, чтобы сложить два отрицательных числа, необходимо найти модули слагаемых и сложить их; перед полученным числом поставить знак «-».
- для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо отдельно выполнить сложение (вычитание) целых частей и отдельно дробных частей, то есть сложить (вычесть) числители дробей, а знаменатель оставить прежним.
- при вычислениях, если возможно, выполняем сокращение обыкновенных дробей.
а) -23+72+37-21-36+51=(72+37+51)-(23+21+36)=160-80=80
б) 3,26-4,34-4,01+6,28+1,36-5,55=(3,26+6,28+1,36)-(4,34+4,01+5,55)=10,9-13,9=-(13,9-10,9)=-3
в) 3 1/3+5 1/6-2 5/8-7 1/4-1 1/8=(3 1/3+5 1/6)-(2 5/8+7 1/4+1 1/8)=(3 (1•2)/(3•2)+5 1/6)-(2 5/8+7 (1•2)/(4•2)+1 1/8)=(3 2/6+5 1/6)-(2 5/8+7 2/8+1 1/8)=((3+5)+(2/6+1/6))-((2+7+1)+(5/8+2/8+1/8))=(8+(2+1)/6)-(10+(5+2+1)/8)=8 3/6-10 8/8=8 (3•1)/(2•3)-10 (2•4)/(2•4)=8 1/2-10 2/2=-(10 2/2-8 1/2)=-((10-8)+(2/2-1/2))=-(2+(2-1)/2)=-2 1/2=-2 (1•5)/(2•5)=-2 5/10=-2,5
г) 0,7-7/12-1/6+0,5-1/4+0,3=(0,7+0,5+0,3)-(7/12+1/6+1/4)=1,5-(7/12+(1•2)/(6•2)+(1•3)/(4•3))=1,5-(7/12+2/12+3/12)=1,5-(7+2+3)/12=1,5-12/12=1,5-1=0,5
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









