Упр.4.288 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
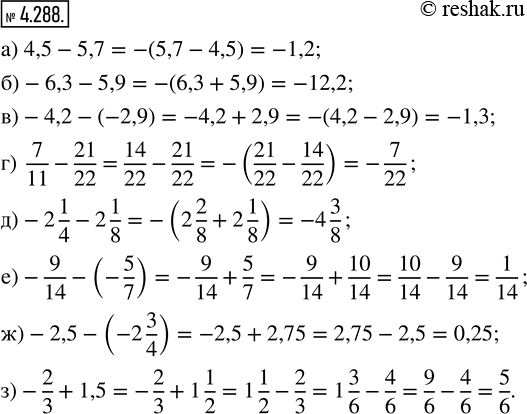
Решение #2 (Учебник 2023)

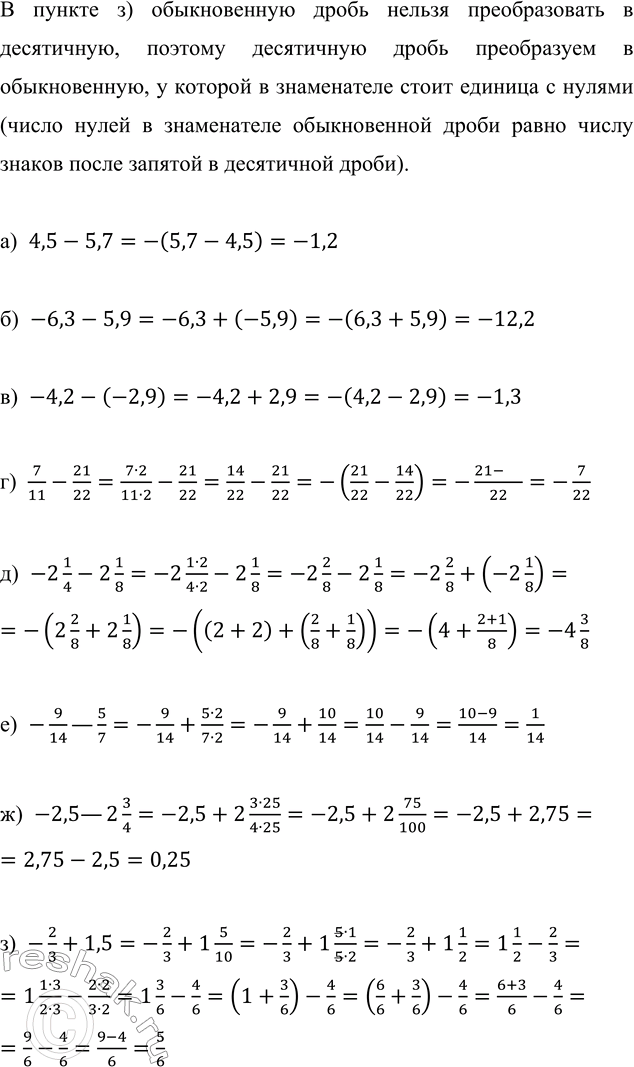
Решение #3 (Учебник 2023)
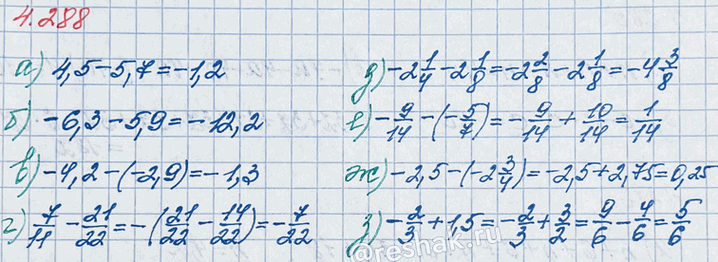
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Вычислите:
а) 4,5 - 5,7; в) -4,2 - (-2,9); д) -2 1/4 - 2 1/8; ж) -2,5 - (-2 3/4);
б) -6,3 - 5,9; г) 7/11 - 21/22; е) -9/14 - (-5/7); з) -2/3 + 1,5.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы сложить два числа с разными знаками, необходимо найти модули слагаемых; из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем.
- для того, чтобы сложить два отрицательных числа, необходимо найти модули слагаемых; сложить модули слагаемых; перед полученным числом поставить знак «-».
- для того, чтобы из данного числа вычесть другое, необходимо к уменьшаемому прибавить число, противоположное вычитаемому.
- для того, чтобы сложить (вычесть) две дроби с разными знаменателями, необходимо привести данные дроби к общему знаменателю; применить правило сложения (вычитания) дробей с одинаковыми знаменателями, то есть сложить (вычесть) их числители, а знаменатель оставить прежним.
- для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо привести дробные части этих чисел к наименьшему общему знаменателю; отдельно выполнить сложение (вычитание) целых частей и отдельно дробных частей.
В пунктах ж) и з), чтобы выполнить вычисления дроби, необходимо привести к одному виду, либо к десятичным, либо к обыкновенным.
В пункте ж) обыкновенную дробь переводим в десятичную, для этого числитель и знаменатель умножаем на 25 (основное свойство дроби – если числитель и знаменатель дроби умножить на одно и то же число, то получится дробь, равная данной).
В пункте з) обыкновенную дробь нельзя преобразовать в десятичную, поэтому десятичную дробь преобразуем в обыкновенную, у которой в знаменателе стоит единица с нулями (число нулей в знаменателе обыкновенной дроби равно числу знаков после запятой в десятичной дроби).
а) 4,5-5,7=-(5,7-4,5)=-1,2
б) -6,3-5,9=-6,3+(-5,9)=-(6,3+5,9)=-12,2
в) -4,2-(-2,9)=-4,2+2,9=-(4,2-2,9)=-1,3
г) 7/11-21/22=(7•2)/(11•2)-21/22=14/22-21/22=-(21/22-14/22)=-(21-14)/22=-7/22
д) -2 1/4-2 1/8=-2 (1•2)/(4•2)-2 1/8=-2 2/8-2 1/8=-2 2/8+(-2 1/8)=-(2 2/8+2 1/8)=-((2+2)+(2/8+1/8))=-(4+(2+1)/8)=-4 3/8
е) -9/14—5/7=-9/14+(5•2)/(7•2)=-9/14+10/14=10/14-9/14=(10-9)/14=1/14
ж) -2,5—2 3/4=-2,5+2 (3•25)/(4•25)=-2,5+2 75/100=-2,5+2,75=2,75-2,5=0,25
з) -2/3+1,5=-2/3+1 5/10=-2/3+1 (5•1)/(5•2)=-2/3+1 1/2=1 1/2-2/3=1 (1•3)/(2•3)-(2•2)/(3•2)=1 3/6-4/6=(1+3/6)-4/6=(6/6+3/6)-4/6=(6+3)/6-4/6=9/6-4/6=(9-4)/6=5/6
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









