Упр.2.241 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
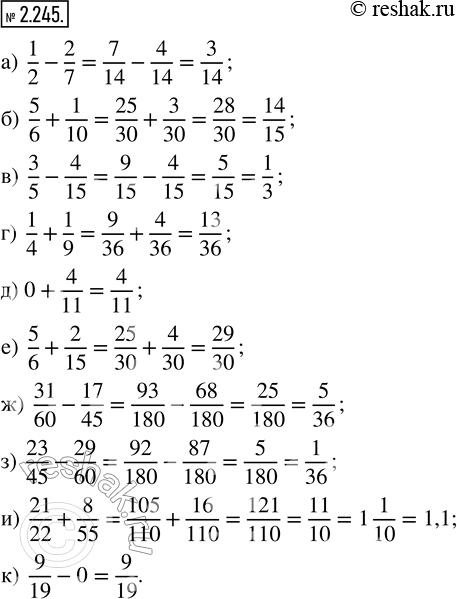
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
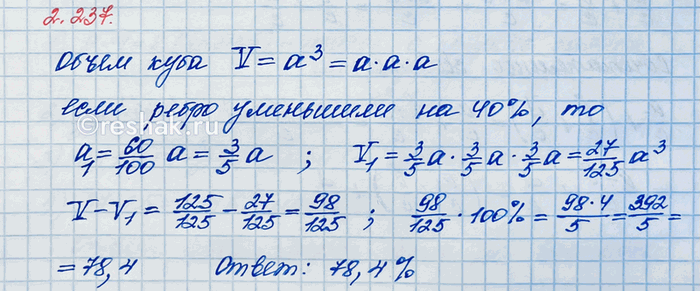
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Вычислите:
а) 1/2 - 2/7; в) 3/5 - 4/15; д) 0 + 4/11; ж) 31/60 - 17/45; и) 21/22 + 8/55;
б) 5/6 + 1/10; г) 1/4 + 1/9; е) 5/6 + 2/15; з) 23/45 - 29/60; к) 9/19 - 0.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают (вычитают), а знаменатель оставляют тот же.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь равная данной.
Если в ответе получается сократимая дробь, необходимо числитель и знаменатель разделить на одно и то же число.
Если при вычислениях получается неправильная дробь, то есть дробь, у которой числитель больше знаменателя, то необходимо числитель разделить на знаменатель с остатком, далее целое записать в целую часть смешанного числа, остаток записать в числитель дроби, а знаменатель оставить тот же.
а) 1/2-2/7=(1•7)/(2•7)-(2•2)/(7•2)=7/14-4/14=(7-4)/14=3/14
б) 5/6+1/10=(5•5)/(6•5)+(1•3)/(10•3)=25/30+3/30=(25+3)/30=28/30=(2•14)/(2•15)=14/15
в) 3/5-4/15=(3•3)/(5•3)-4/15=9/15-4/15=(9-4)/15=5/15=(5•1)/(5•3)=1/3
г) 1/4+1/9=(1•9)/(4•9)+(1•4)/(9•4)=9/36+4/36=(9+4)/36=13/36
д) 0+4/11=4/11
е) 5/6+2/15=(5•5)/(6•5)+(2•2)/(15•2)=25/30+4/30=(25+4)/30=29/30
ж) 31/60-17/45=(31•3)/(60•3)-(17•4)/(45•4)=93/180-68/180=(93-68)/180=25/180=(5•5)/(5•36)=5/36
з) 23/45-29/60=(23•4)/(45•4)-(29•3)/(60•3)=92/180-87/180=(92-87)/180=5/180=(5•1)/(5•36)=1/36
и) 21/22+8/55=(21•5)/(22•5)+(8•2)/(55•2)=105/110+16/110=(105+16)/110=121/110=(11•11)/(11•10)=11/10=1 1/10
к) 9/19-0=9/19
Каждое ребро куба уменьшили на 40 %. На сколько процентов уменьшится объём куба?
Для того, чтобы найти на сколько уменьшился объём куба в процентах, необходимо сравнить его с изначальным объёмом, для этого нужно из первоначального объёма (100%) вычесть получившийся объём (21,6%).
Пусть ребро куба было a см.
Тогда, объём первоначального куба V=a^3 - это 100%.
Ребро куба уменьшили на 40%, то есть длина ребра стала
a-0,4a=0,6a.
Найдём объём куба с уменьшенным ребром.
V=(0,6a)^3=0,216a^3 - объём куба с ребром 0,6a.
0,216a^3=0,216•100%=21,6% - объём нового куба в процентах от первоначального объёма.
100%-21,6%=78,4% - на столько процентов уменьшился объём нового куба.
Ответ: на 78,4%.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.