Проверь себя Глава 4 ГДЗ Колягин Ткачёва 11 класс (Алгебра)
Решение #1
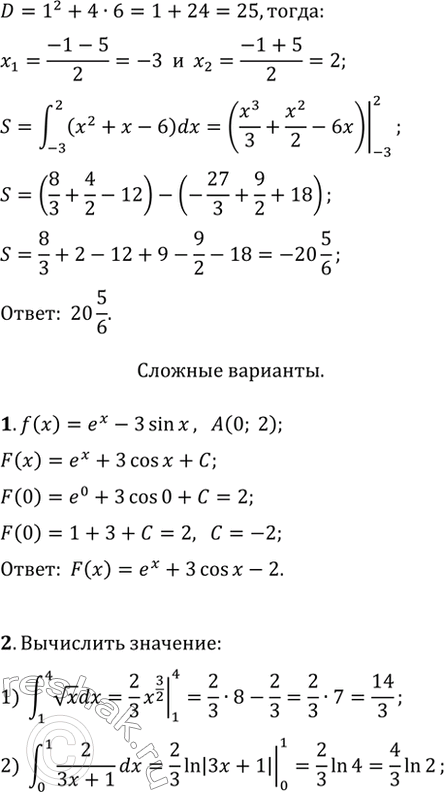
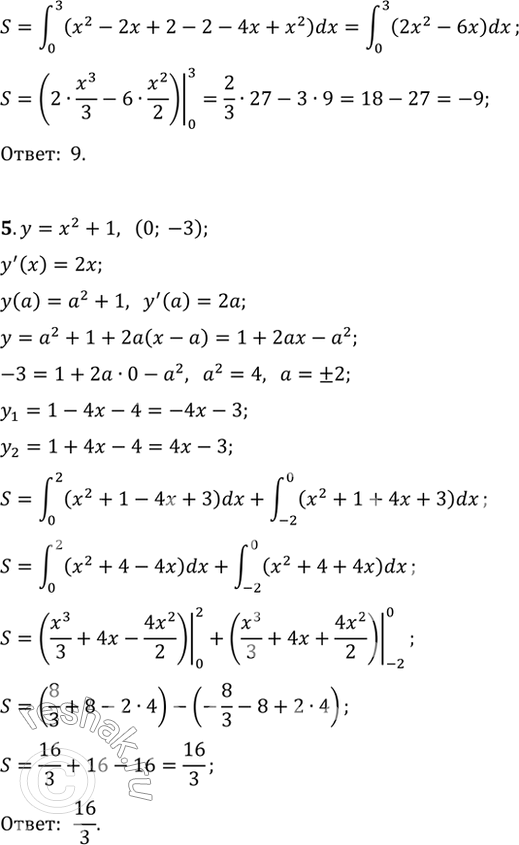
Решение #2
Рассмотрим вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 11 класс, Просвещение:
1. Показать, что F(x) = e2x + x3- cosx является первообразной для функции f(x) = 2е3х + 3х2 + sinx на всей числовой прямой.
2. Для функции f(x) = 3х2 + 2х - 3 найти первообразную, график которой проходит через точку М( 1; -2).
3. Вычислить:
1) интеграл (1;2) 2x2dx;
2) интеграл (2;3) dx/x3;
3) интеграл (0;пи/2) cos2xdx;
4) интеграл (пи/2;пи) sinxdx.
4. Найти площадь фигуры, ограниченной параболой у = х2 + + х - 6 и осью Ох.
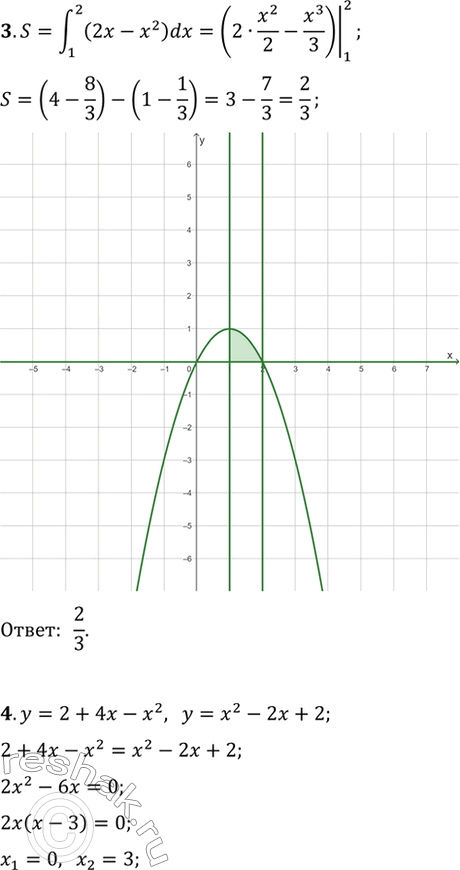
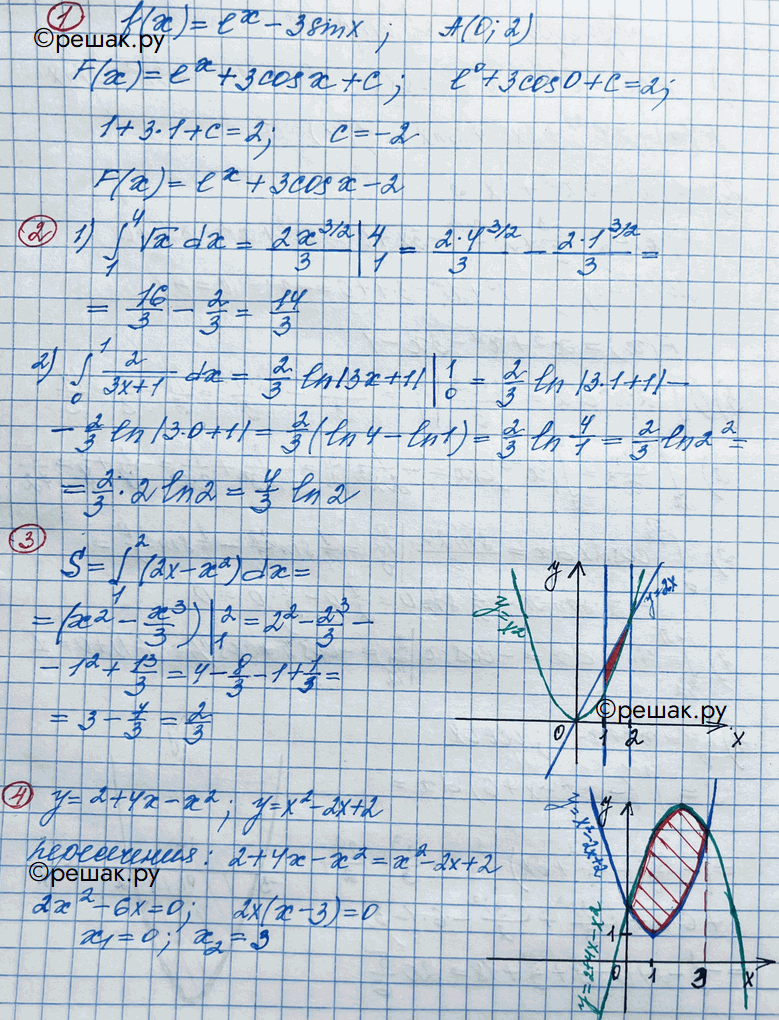
1. Для функции f(x) = еx - 3sin х найти первообразную, график которой проходит через точку А(0; 2).
2. Вычислить:
1) интеграл (1;4) корень x dx;
2) интеграл (0;1) 2/3x+1 dx.
3. Изобразить фигуру, площадь которой равна интеграл (1;2) (2х-x2)dx, и вычислить эту площадь.
4. Найти площадь фигуры, ограниченной линиями
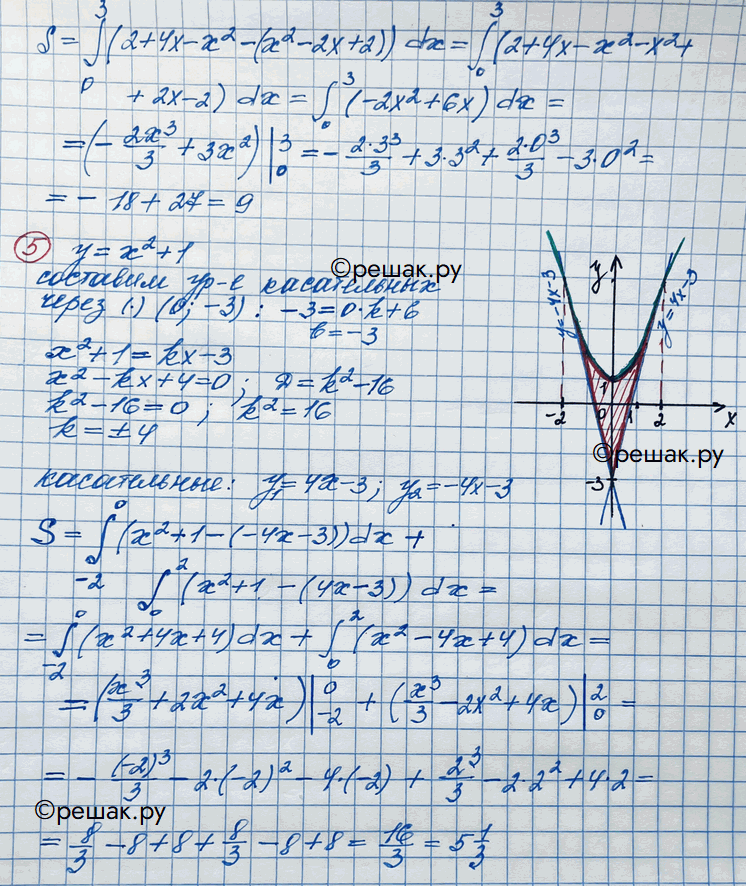
у = 2 + 4х - х2 и у = х2 - 2х + 2.
5. Найти площадь фигуры, ограниченной параболой у = х2 + 1 и касательными к ней, проведёнными из точки (0; -3).
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
