Упр.4.394 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
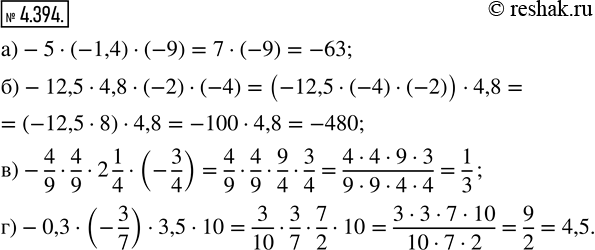
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)
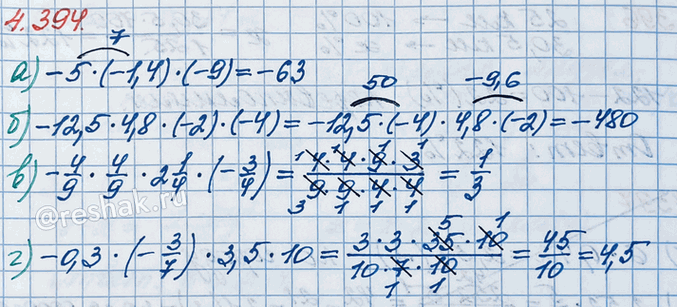
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действия:
а) -5 · (-1,4) · (-9); в) -4/9 · 4/9 · 2 1/4 · (-3/4);
б) -12,5 · 4,8 · (-2) · (-4); г) -0,3 · (-3/7) · 3,5 · 10.
Для того, чтобы перемножить два отрицательных числа, необходимо перемножить их модули, то есть произведение двух отрицательных чисел является положительным числом, тогда, если в произведении чётное количество отрицательных множителей, то произведение будет положительным числом; если в произведении нечётное количество отрицательных множителей, то произведение будет отрицательным числом.
При выполнении вычислений используем переместительное и сочетательное свойства умножения, то есть меняем множители местами и расставляем скобки так, чтобы вычисления были проще.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы умножить десятичную дробь на натуральное число, необходимо умножить их как натуральные числа, не обращая внимание на запятую; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой у умножаемой дроби.
- для того, чтобы умножить десятичную дробь на 100, необходимо в этой дроби перенести запятую вправо на две цифры.
- для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменений.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведением знаменателей.
- для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
- при вычислениях с обыкновенными дробями, если возможно, выполняем сокращение.
а) -5•(-1,4)•(-9)=5•1,4•(-9)=7•(-9)=-63
б) -12,5•4,8•(-2)•(-4)=-12,5•(-4)•(-2)•4,8=-12,5•8•4,8=-100•4,8=-480
в) -4/9•4/9•2 1/4•(-3/4)=4/9•4/9•9/4•3/4=(4•4•9•3)/(9•3•3•4•4)=1/3
г) -0,3•(-3/7)•3,5•10=3/10•3/7•35/10•10/1=(3•3•5•7•10)/(10•7•2•5)=9/2=4,5
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









