Упр.4.395 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
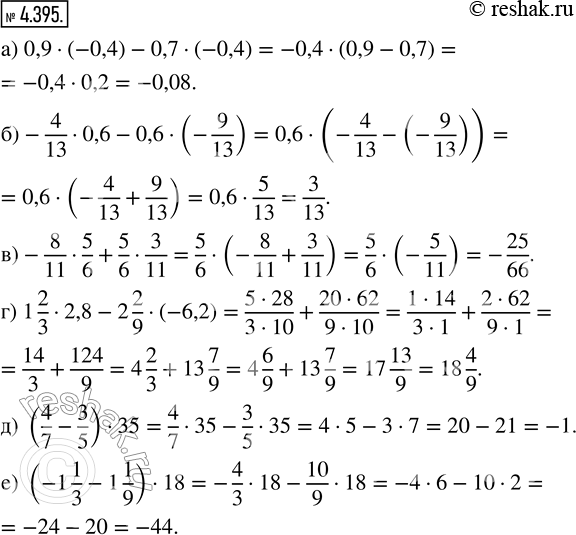
Решение #2 (Учебник 2023)


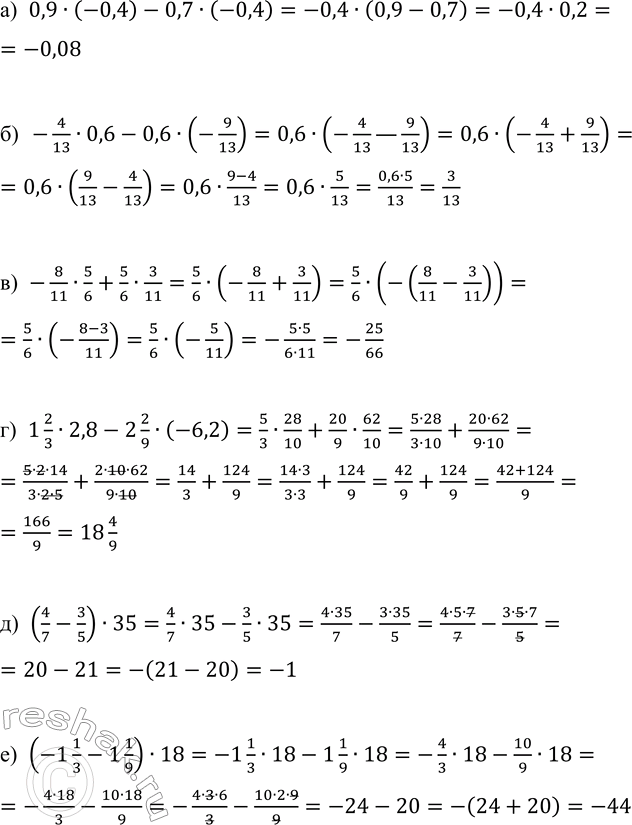
Решение #3 (Учебник 2023)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите значение выражения:
а) 0,9 · (-0,4) - 0,7 · (-0,4); г) 1 2/3 · 2,8 - 2 2/9 · (-6,2);
б) -4/13 · 0,6 - 0,6 · (-9/13); д) (4/7 - 3/5) · 35;
в) -8/11 · 5/6 + 5/6 · 3/11; е) (-1 1/3 - 1 1/9) · 18.
При выполнении вычислений используем распределительное свойство умножения, то есть в пунктах а, б и в выносим одинаковые множители за скобки, затем выполняем вычисления в скобках и умножаем полученный на вынесенный множитель, а в пунктах д и е, наоборот, раскрываем скобки, умножая каждый из компонентов, стоящий в скобках, затем складываем полученные произведения.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы перемножить два числа с разными знаками, необходимо умножить их модули и перед полученным произведением поставить знак «-».
- для того, чтобы перемножить два отрицательных числа, необходимо перемножить их модули.
- для того, чтобы из данного числа вычесть другое, необходимо к уменьшаемому прибавить число, противоположное вычитаемому.
- для того, чтобы перемножить две десятичные дроби, необходимо умножить их как натуральные числа, не обращая внимание на запятые; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
- для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- для того, чтобы сложить числа с разными знаками, необходимо найти модули слагаемых и из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем.
- для того, чтобы сложить два отрицательных числа, необходимо найти и сложить модули слагаемых; перед полученным числом поставить знак «-».
- для того, чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведением знаменателей.
- для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
- при вычислениях с обыкновенными дробями, если возможно, выполняем сокращение.
а) 0,9•(-0,4)-0,7•(-0,4)=-0,4•(0,9-0,7)=-0,4•0,2=-0,08
б) -4/13•0,6-0,6•(-9/13)=0,6•(-4/13—9/13)=0,6•(-4/13+9/13)==0,6•(9/13-4/13)=0,6•(9-4)/13=0,6•5/13=(0,6•5)/13=3/13
в) -8/11•5/6+5/6•3/11=5/6•(-8/11+3/11)=5/6•(-(8/11-3/11))=5/6•(-(8-3)/11)=5/6•(-5/11)=-(5•5)/(6•11)=-25/66
г) 1 2/3•2,8-2 2/9•(-6,2)=5/3•28/10+20/9•62/10=(5•28)/(3•10)+(20•62)/(9•10)=(5•2•14)/(3•2•5)+(2•10•62)/(9•10)=14/3+124/9=(14•3)/(3•3)+124/9=42/9+124/9=(42+124)/9=166/9=18 4/9
д) (4/7-3/5)•35=4/7•35-3/5•35=(4•35)/7-(3•35)/5=(4•5•7)/7-(3•5•7)/5=20-21=-(21-20)=-1
е) (-1 1/3-1 1/9)•18=-1 1/3•18-1 1/9•18=-4/3•18-10/9•18=-(4•18)/3-(10•18)/9=-(4•3•6)/3-(10•2•9)/9=-24-20=-(24+20)=-44
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









