Упр.3.86 ГДЗ Сборник упражнений Босова 7-9 класс (Информатика)
Решение #1




Рассмотрим вариант решения задания из учебника Босова, Аквилянов 9 класс, Просвещение:
3.86. Исполнитель Робот действует на клетчатом поле, между клетками которого могут быть стены.
1) На бесконечном клетчатом поле имеется горизонтальная стена. Длина стены неизвестна. Робот находится в одной из клеток, примыкающих к стене сверху. На рисунке указан один из возможных вариантов расположения Робота и стены (Робот обозначен буквой «Р»).
Робот должен закрасить все клетки, примыкающие к стене сверху. Так, для приведенного выше рисунка должны быть закрашены следующие клетки:
Конечное положение Робота значения не имеет.
Опишите укрупненными блоками план действий Робота по решению поставленной задачи:
1. Найти конец стены.
2. Встать на первую клетку над стеной.
3. Закрасить все клетки, прилегающие к стене.
4. ВСЕ
2) Где-то в поле Робота находятся две вертикальные стены равной, но неизвестной длины, расположенные одна напротив другой. Робот находится в произвольной клетке справа от правой стены, причем напротив нее.
На рисунке указан один из возможных вариантов рас-положения Робота и стен (Робот обозначен буквой «Р»).
Робот приступил к исполнению следующего алгоритма
Каким будет результат исполнения данного алгоритма. Изобразите его на рисунке.
Опишите алгоритм действий Робота укрупненными шагами.
1. Подойти к правой стене.
2. Подняться по стене до верхнего ее конца.
3. Закрасить все клетки между стенами.
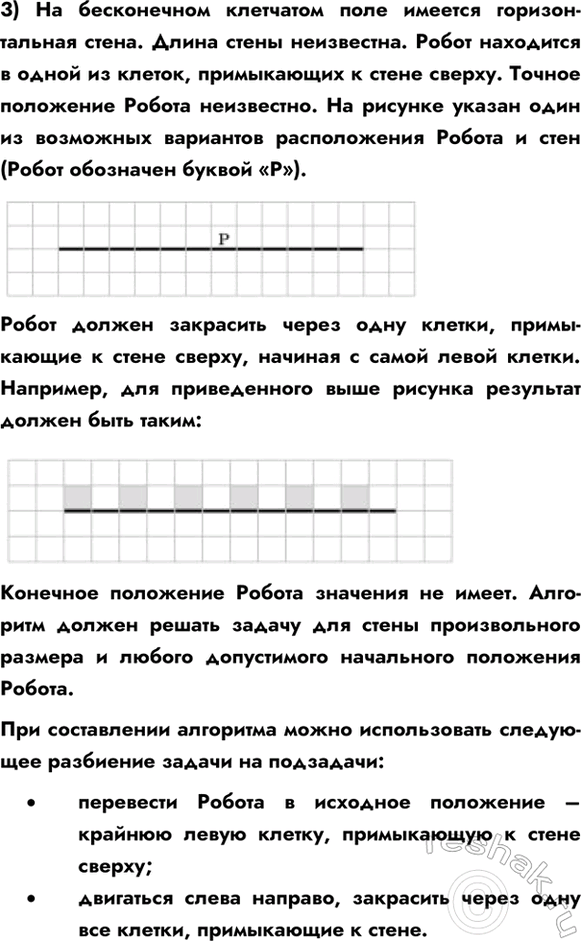
3) На бесконечном клетчатом поле имеется горизонтальная стена. Длина стены неизвестна. Робот находится в одной из клеток, примыкающих к стене сверху. Точное положение Робота неизвестно. На рисунке указан один из возможных вариантов расположения Робота и стен (Робот обозначен буквой «Р»).
Робот должен закрасить через одну клетки, примыкающие к стене сверху, начиная с самой левой клетки. Например, для приведенного выше рисунка результат должен быть таким:
Конечное положение Робота значения не имеет. Алгоритм должен решать задачу для стены произвольного размера и любого допустимого начального положения Робота.
При составлении алгоритма можно использовать следующее разбиение задачи на подзадачи:
• перевести Робота в исходное положение – крайнюю левую клетку, примыкающую к стене сверху;
• двигаться слева направо, закрасить через одну все клетки, примыкающие к стене.
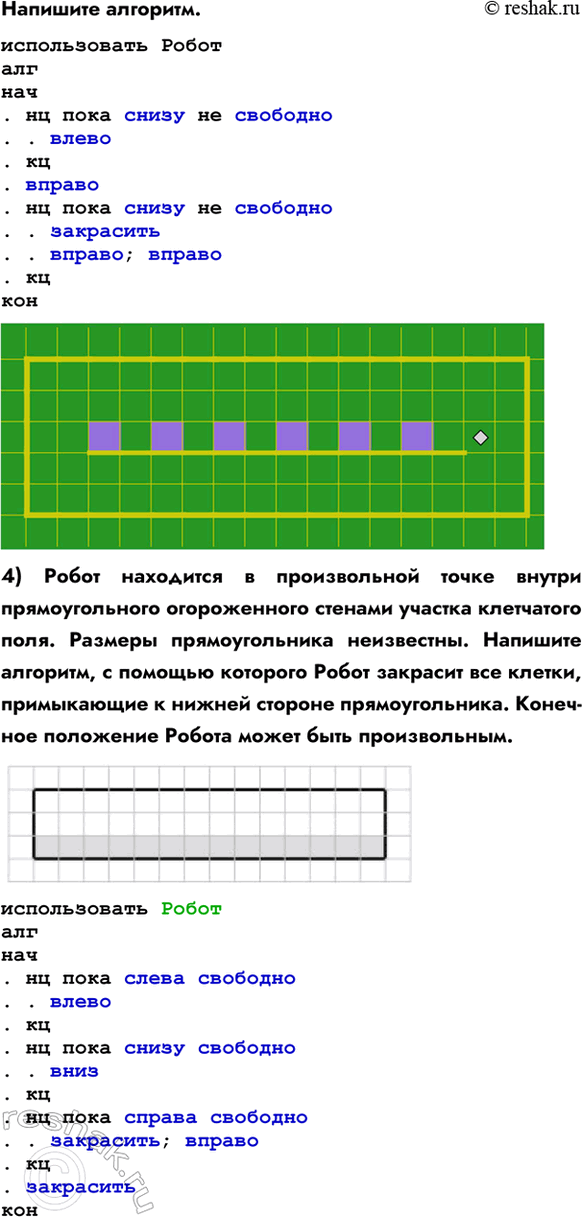
Напишите алгоритм.
использовать Робот
алг
нач
. нц пока снизу не свободно
. . влево
. кц
. вправо
. нц пока снизу не свободно
. . закрасить
. . вправо; вправо
. кц
кон
4) Робот находится в произвольной точке внутри прямоугольного огороженного стенами участка клетчатого поля. Размеры прямоугольника неизвестны. Напишите алгоритм, с помощью которого Робот закрасит все клетки, примыкающие к нижней стороне прямоугольника. Конечное положение Робота может быть произвольным.
использовать Робот
алг
нач
. нц пока слева свободно
. . влево
. кц
. нц пока снизу свободно
. . вниз
. кц
. нц пока справа свободно
. . закрасить; вправо
. кц
. закрасить
кон
5) Робот находится в произвольной точке внутри прямоугольного огороженного стенами участка клетчатого поля. Размеры прямоугольника неизвестны. Напишите алгоритм, с помощью которого Робот закрасит все клетки, примыкающие к сторонам прямоугольника, и вернется в начальное положение.
Для запоминания начального положения Робота введены две переменные: k1 и k2
использовать Робот
алг
нач
. цел k1,k2
. k1:=0; k2:=0;
. нц пока слева свободно
. . влево
. . k1:=k1+1
. кц
. нц пока снизу свободно
. . вниз
. . k2:=k2+1
. кц
. нц пока справа свободно
. . закрасить; вправо
. кц
. закрасить
. нц пока сверху свободно
. . вверх; закрасить
. кц
. нц пока слева свободно
. . влево; закрасить
. кц
. нц пока снизу свободно
. . вниз; закрасить
. кц
. нц k1 раз
. . вправо
. кц
. нц k2 раз
. . вверх
. кц
кон
Популярные решебники 9 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.





