Упр.366 ГДЗ Атанасян 10-11 класс по геометрии (Геометрия)
Решение #1

Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 10 класс, Просвещение:
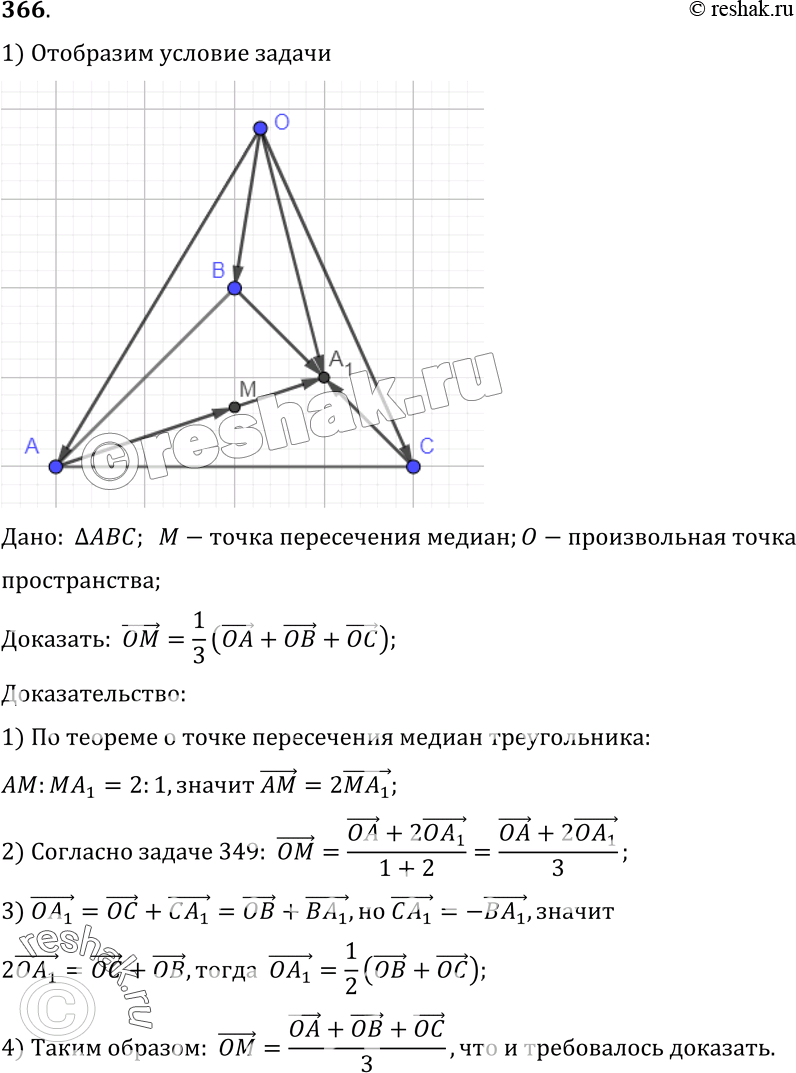
366 Докажите, что если M — точка пересечения медиан треугольника ABC, а 0 — произвольная точка пространства, то
OM = I {OA. + OB + ОС).
Решение
По теореме о точке пересечения медиан треугольника AM = 2MA1, где AA1 — медиана треугольника ABC (рис. 117). Согласно за-
o лс\ г\\я 0A + 20Ai OA + 20А1 тт
даче 349 OM =-l- =-J-. Ho
_> _* 1+2 3 OA,=|(OB + OC) (объясните почему), поэтому OM = ОА + ОВ+ОС
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением





