Упр.1.26 ГДЗ Мордковича 10 класс профильный уровень (Алгебра)
Решение #1
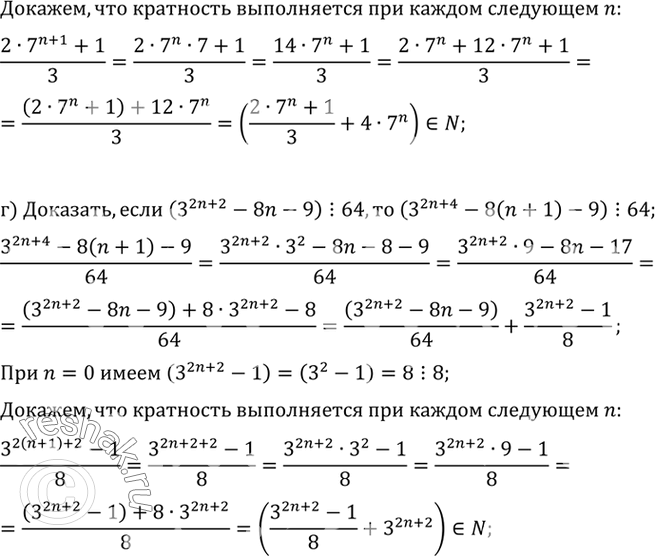
Решение #2(записки учителя)
Решение #3(записки школьника)
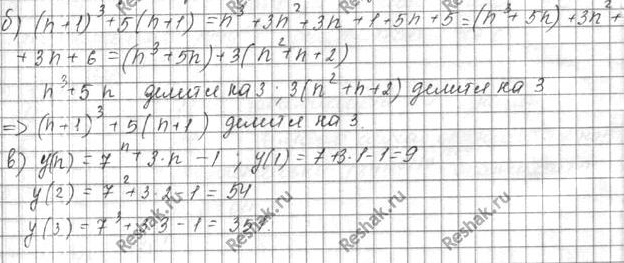
Рассмотрим вариант решения задания из учебника Мордкович, Семенов 10 класс, Мнемозина:
1.25. а) Докажите, что если при некотором натуральном значении n число n3 - n делится на 6, то и число (n + 1 3 - (n + 1) ткже делится на 6. Проверьте наличие делимости для n = 1) и подумайте, для каких еще значений n имеет место делимость.
б) Докажите, что если при некотором натуральном значении n число n3 + 5n делится на 6, то и число (n + 1 3 + + 5(n + 1) также делится на 6. Проверьте наличие делимости для n = 1 и подумайте, для каких еще значений n имеет место делимость.
в) Докажите, что если при некотором натуральном значении n число 7n + 3n - 1 делится на 9, то и число 7n + 1 + 3(n + 1) - 1 также делится на 9. Проверьте наличие делимости для n = 1 и подумайте, для каких еще значений n имеет место делимость.
г) Докажите, что если при некотором натуральном значении n число 32n+2 - 8n - 9 делится на 64, то и число 32n+4 - 8(n + 1) - 9 также делится на 64. Проверьте наличие делимости для n = 1 и подумайте, для каких еще значений n имеет место делимость.
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением