Упр.595 ГДЗ Макарычев Миндюк 9 класс (Алгебра)
Решение #1

Решение #2

Решение #3
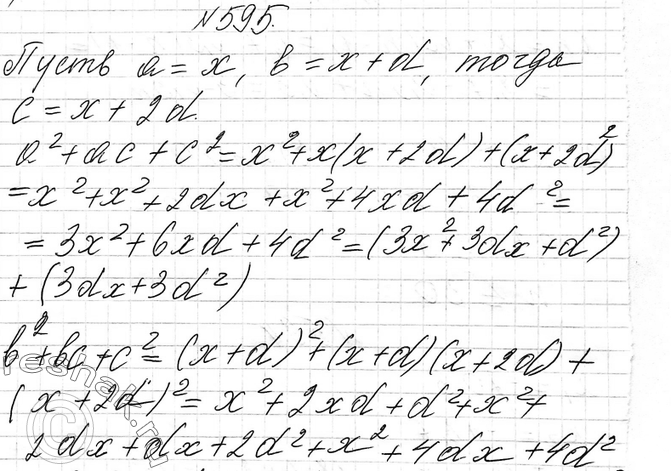
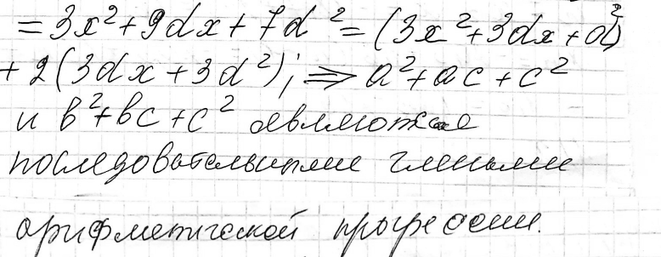

Рассмотрим вариант решения задания из учебника Макарычев, Миндюк, Нешков 9 класс, Просвещение:
595 Докажите, что если числа а, b, с являются последовательными членами арифметической прогрессии, то числа а2 + ab + b2, а2 + ас + с2 и b2 + bс + с2 также являются последовательными членами некоторой арифметической прогрессии.
Похожие решебники
Популярные решебники 9 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






