Самостоятельная работа 19 Вариант 2 ГДЗ Дидактические материалы Никольский Потапов 10 класс (Алгебра)
Решение #1
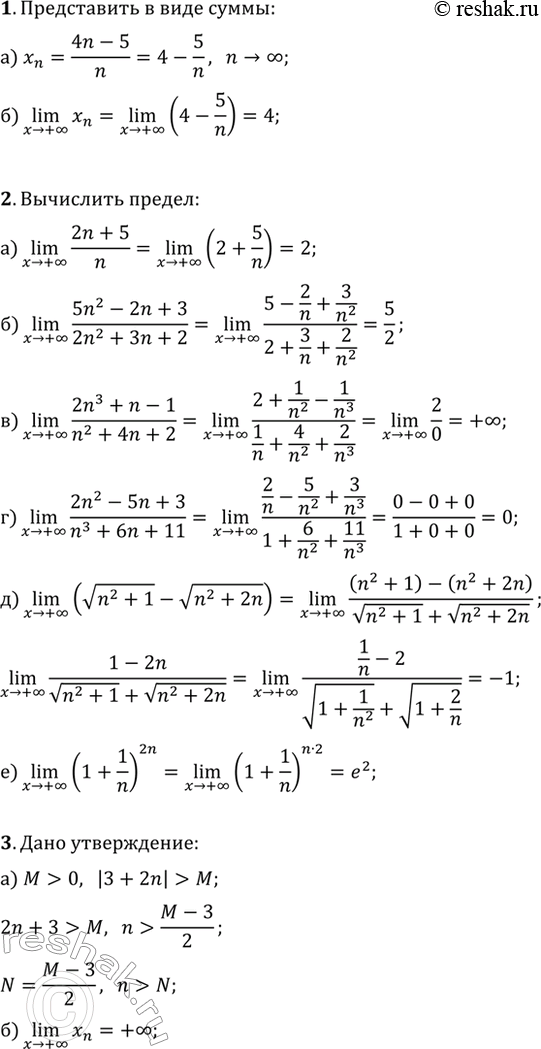

Рассмотрим вариант решения задания из учебника Потапов, Шевкин, Никольский 10 класс, Просвещение:
1. а) Представьте переменную x_n=(4n-5)/n в виде суммы числа и бесконечно малой.
б) Чему равен (n > +?)lim(x_n)?
2. Пользуясь свойствами пределов, вычислите предел:
а) (n > +?)lim((2n+5)/n); б) (n > +?)lim((5n^2-2n+3)/(2n^2+3n+2));
в) (n > +?)lim((2n^3+n-1)/(n^3+4n+2)); г) (n > +?)lim((2n^2-5n+3)/(n^3+6n+11));
д) (n > +?)lim(v(n^2+1)-v(n^2+2n)); е) (n > +?)lim(1+1/n)^(2n).
3. а) Докажите, что переменная x_n=3+2n является бесконечно большой, пользуясь определением бесконечно большой (на языке «М-N»).
б) Чему равен (n > +?)lim(x_n)?
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






