Итоговый тест Вариант 1 ГДЗ Дидактические материалы Никольский Потапов 10 класс (Алгебра)
Решение #1
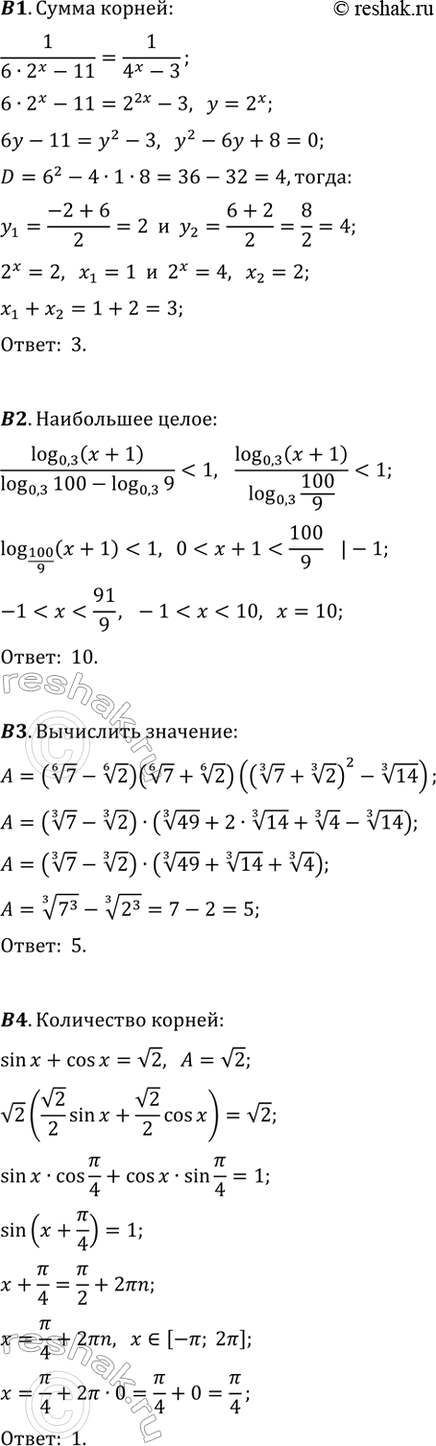
Рассмотрим вариант решения задания из учебника Потапов, Шевкин, Никольский 10 класс, Просвещение:
А1. Упростите выражение a^(1/4):a^(-1/2).
1) a^(1/4); 2) (a^3)^(1/4); 3) 1/a^(1/4); 4) 1/(a^3)^(1/4).
А2. Упростите выражение (b^(2/5)-25)/(b^(1/5)+5)-b^(1/5).
1) -5; 2) 5; 3) b^(2/5); 4) b^(-2/5).
А3. Упростите выражение log(3; 18)-log(3; 2)+5^log(5; 2).
1) log(3; 2); 2) 0; 3) 4; 4) -log(3; 2).
А4. Решите неравенство (1/2)^(x-2) > 1/8.
1) (5; +?); 2) (-?; 5); 3) (-?; 1); 4) (1; +?).
А5. Укажите промежуток возрастания функции y=f(x), заданной графиком (рис. 42).
1) [-3; 0]; 2) [-4; 3]; 3) [-2; 2]; 4) [0; 3].
А6. Упростите выражение 2cos^(?/2)-cos(?)-1.
1) 2cos^2(?/2); 2) 2sin^2(?/2); 3) 2; 4) 0.
А7. Решите уравнение log(2; x)=1/2.
1) 1/2; 2) 2; 3) 4; 4) v2.
А8. Укажите промежуток, которому принадлежит корень уравнения log(2; x-2)=3.
1) (10; 13); 2) (9; 13); 3) (5; 7); 4) (7; 9).
А9. Найдите область определения функции y=v((x-1)/(x+1)).
1) (-?; -1)?[1; +?); 2) (-?; -1)?(1; +?); 3) (-?; -1]?(1; +?); 4) (-1; 1].
А10. Решите неравенство 9^x?1/3.
1) [-0,5; +?); 2) (-?; -0,5]; 3) [-2; +?); 4) (-?; -2).
А11. Решите неравенство 2^(x+2)+2^x > 20.
1) (-?; 2); 2) (-?; 2]; 3) (2; +?); 4) [2; +?).
А12. Найдите произведение корней уравнения lg^2(x)-3lg(x)-10=0.
1) 10; 2) -10; 3) 1/1000; 4) 1000.
А13. Решите уравнение 2cos^2(x)-3sin(x)=0.
1) (-1)^(m+1)•?/6+?m, m?Z; 2) (-1)^m•?/6+2?m, m?Z;
3) ±?/3+2?m, m?Z; 4) (-1)^m•?/6+?m, m?Z.
В1. Найдите сумму корней уравнения 1/(6•2^x-11)=1/(4^x-3).
В2. Найдите наибольшее целое решение неравенства
log(0,3; x+1)/(log(0,3; 100)-log(0,3; 9)) < 1.
В3. Вычислите (7^(1/6)-2^(1/6))(7^(1/6)+2^(1/6))((7^(1/3)+2^(1/3))^2-14^(1/3)).
В4. Сколько корней уравнения sin(x)+cos(x)=v2 принадлежит промежутку [-?; 2?]?
В5. На соревнованиях по кольцевой трассе первый лыжник проходил круг на 2 мин быстрее второго и через час обогнал его на целый круг. За сколько минут первый лыжник проходил один круг?
В6. Вычислите sin(?/6+?), если sin(?)=v3/2 и 0 < ? < ?/2.
В7. Найдите значение выражения (1+cos(2?)-sin(2?))/(cos(?)+cos(?/2+?)), если cos(?)=-1/2.
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением