Самостоятельная работа 11 Вариант 3 ГДЗ Дидактические материалы Никольский Потапов 10 класс (Алгебра)
Решение #1
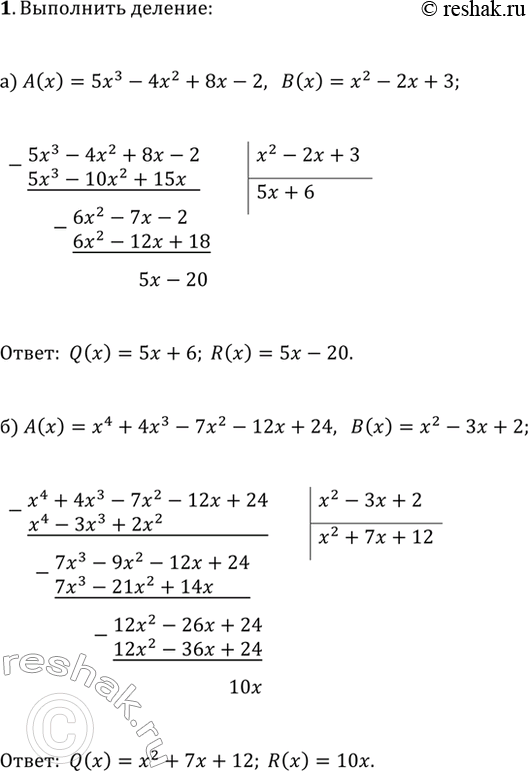
Рассмотрим вариант решения задания из учебника Потапов, Шевкин, Никольский 10 класс, Просвещение:
1. Разделите уголком многочлен А(х) на многочлен В(х), укажите неполное частное Q(x) и остаток R(х), если:
а) A(x)=5x^3-4x^2+8x-2, B(x)=x^2-2x+3;
б) A(x)=x^4+4x^3-7x^2-12x+24, B(x)=x^2-3x+2.
2. С помощью схемы Горнера разделите многочлен А(х) на многочлен В(х), укажите неполное частное Q(x) и остаток В(х), если A(x)=4x^4-13x^2+x, B(x)=x-2.
3. С помощью теоремы Безу определите остаток R(x) от деления многочлена А(х) на многочлен В(х), если:
а) A(x)=6x^3+5x^2-6x+16, B(x)=x+2;
б) A(x)=(x-2)^9, B(x)=x-1.
4. Многочлен P_3(x)=x^3+ax^2+bx-18 при делении на (x+2) дает в остатке 20, а на (x-3) делится без остатка. Определите коэффициенты a и b.
5. Решите уравнение:
а) 3x^3+4x^2-17x-6=0;
б) x^4+x^3-7x^2-x+6=0.
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением