Контрольная работа 3 Вариант 4 ГДЗ Дидактические материалы Никольский Потапов 10 класс (Алгебра)
Решение #1
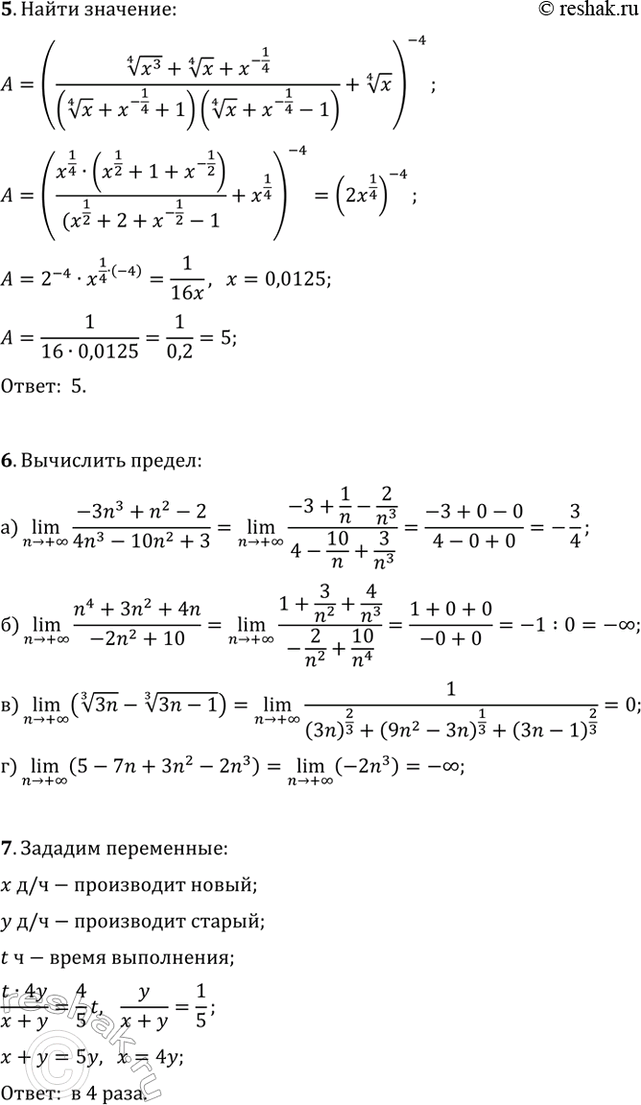

Рассмотрим вариант решения задания из учебника Потапов, Шевкин, Никольский 10 класс, Просвещение:
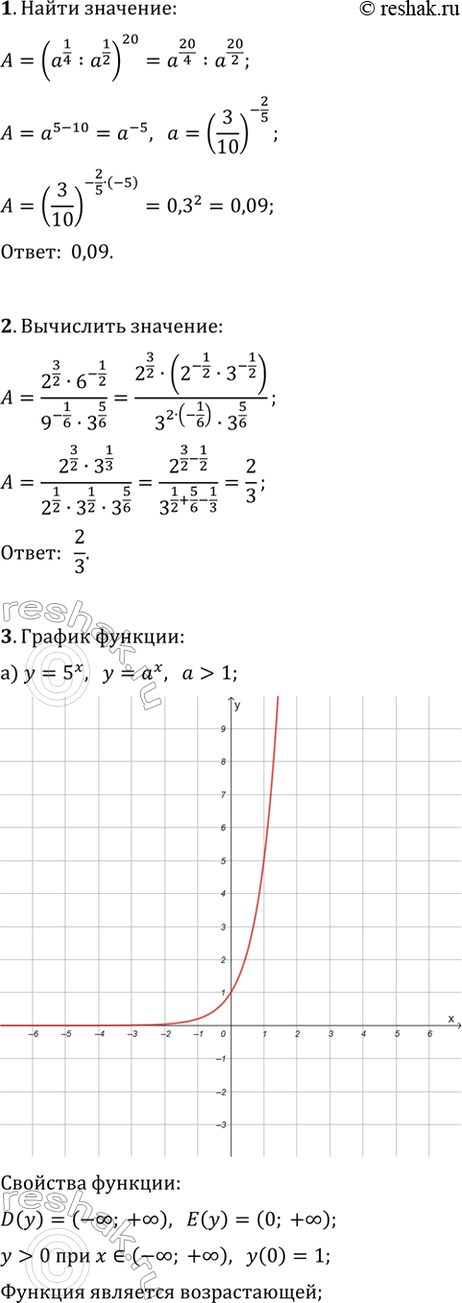
1. Найдите значение выражения (a^(1/4):a^(1/2))^20 при a=(3/10)^(-2/5).
2. Вычислите (2^(3/2)·6^(-1/2))/(9^(-1/6)·3^(5/6)).
3. Постройте график функции и перечислите свойства этой функции:
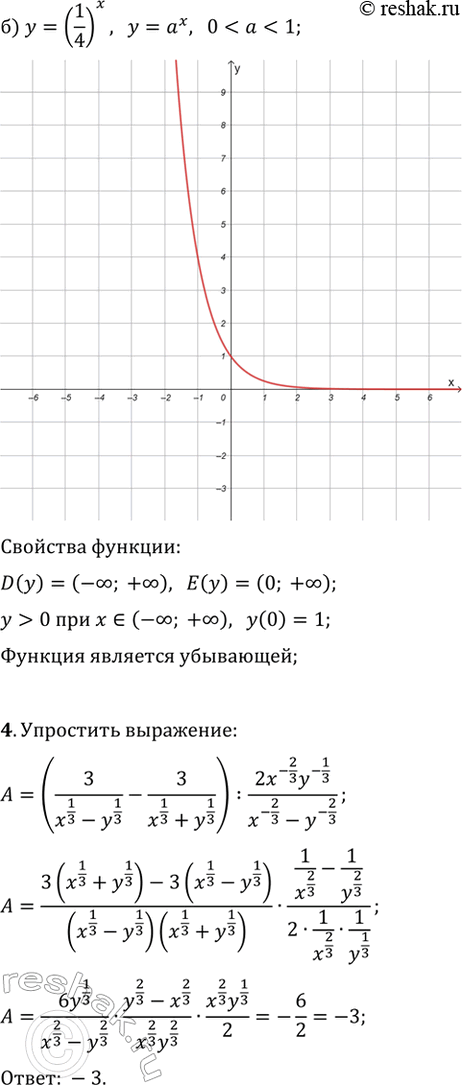
а) y=5^x; б) y=(1/4)^x.
4. Упростите выражение (3/(x^(1/3)-y^(1/3))-3/(x^(1/3)+y^(1/3)))·(2x^(-2/3)y^(-1/3))/(x^(-2/3)-y^(-2/3)).
5*. Упростите выражение (((x^3)^(1/4)+x^(1/4)+x^(-1/4))/((x^(1/4)+x^(-1/4)+1)(x^(1/4)+x^(-1/4)-1))+x^(1/4))^(-4) и найдите его значение при x=0,0125.
6*. Вычислите предел последовательности:
а) (n > +?)lim((-3n^3+n^2-2)/(4n^3-10n^2+3)); б) (n > +?)lim((n^4+3n^2+4n)/(-2n^2+10));
в) (n > +?)lim((3n)^(1/3)-(3n-1)^(1/3)); г) (n > +?)lim(5-7n+3n^2-2n^3).
7*. На четырех старых станках, работающих совместно с одинаковой производительностью, выполнили задание за некоторый срок. На одном новом и одном старом станках, работающих совместно, выполнили бы это задание за 0,8 того же срока. Во сколько раз производительность нового станка больше производительности старого станка?
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






