Контрольная работа 3 Вариант 3 ГДЗ Дидактические материалы Никольский Потапов 10 класс (Алгебра)
Решение #1
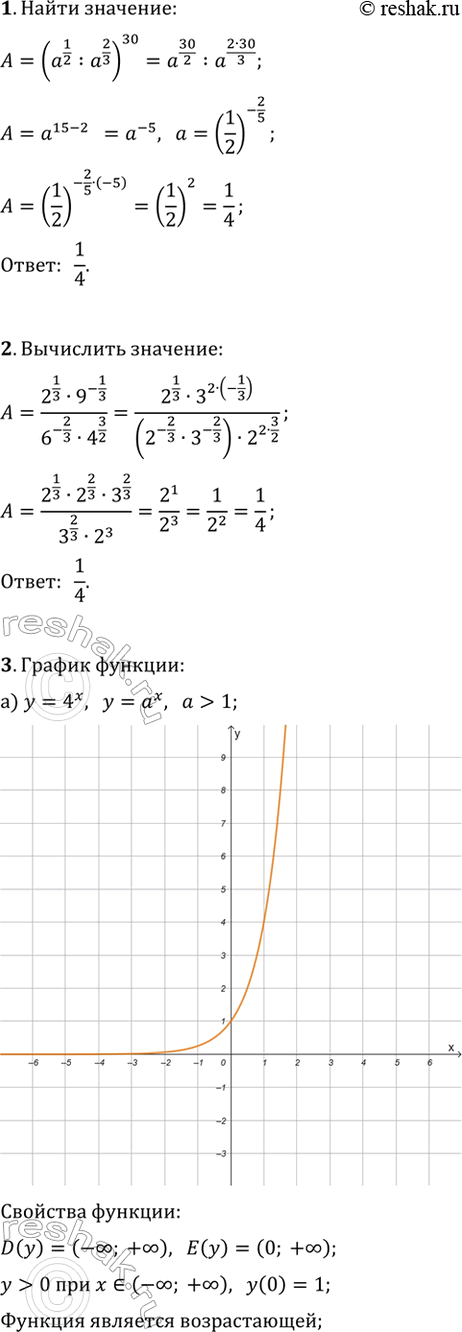
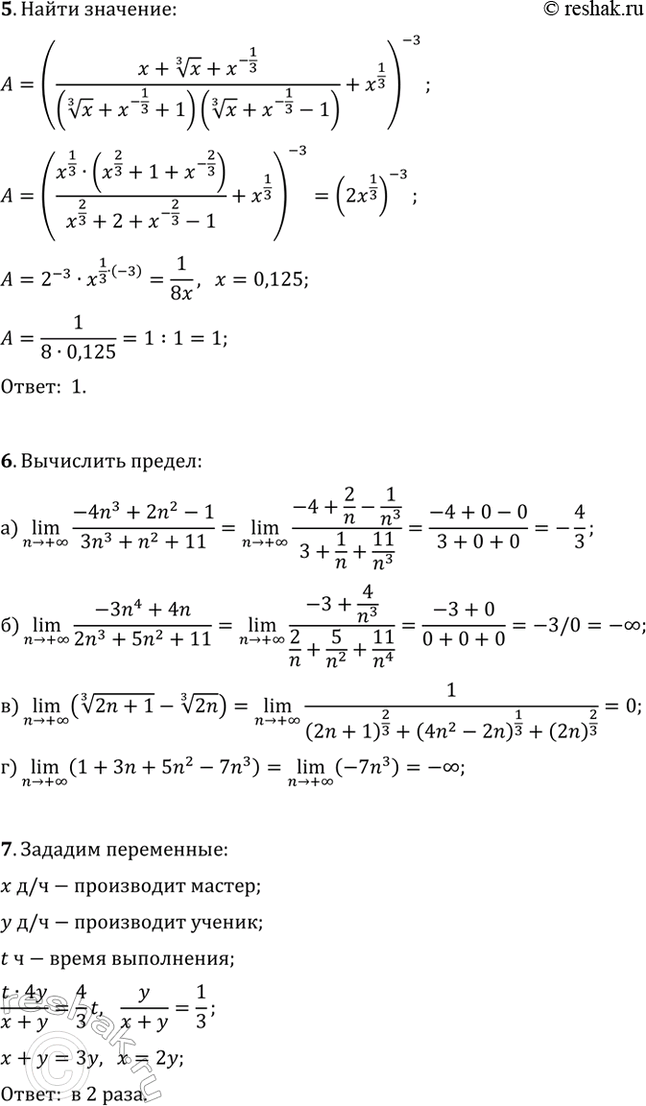

Рассмотрим вариант решения задания из учебника Потапов, Шевкин, Никольский 10 класс, Просвещение:
1. Найдите значение выражения (a^(1/2):a^(2/3))^30 при a=(1/2)^(-2/5).
2. Вычислите (2^(1/3)·9^(-1/3))/(6^(-2/3)·4^(3/2)).
3. Постройте график функции и перечислите свойства этой функции:
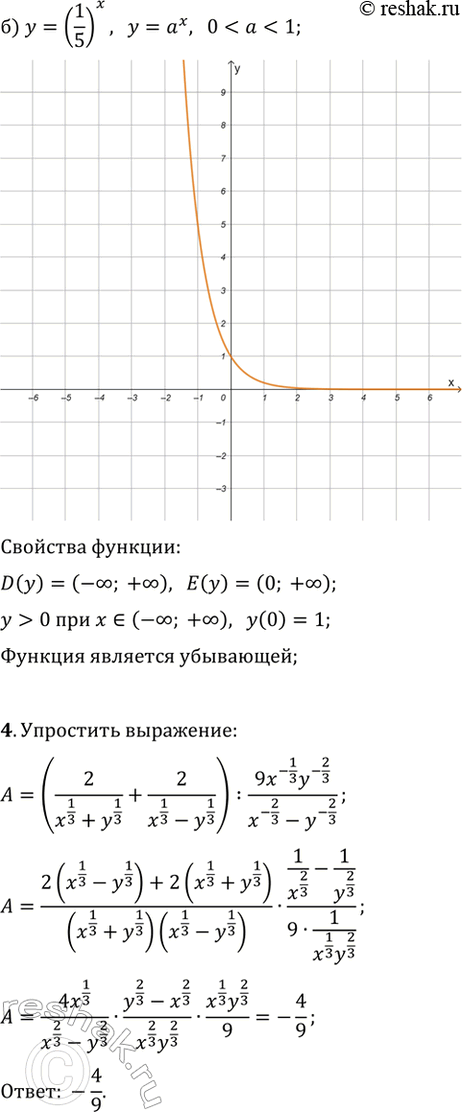
а) y=4^x; б) y=(1/5)^x.
4. Упростите выражение (2/(x^(1/3)+y^(1/3))+2/(x^(1/3)-y^(1/3)))·(9x^(-1/3)y^(-2/3))/(x^(-2/3)-y^(-2/3)).
5*. Упростите выражение ((x+x^(1/3)+x^(-1/3))/((x^(1/3)+x^(-1/3)+1)(x^(1/3)+x^(-1/3)-1))+x^(1/3))^(-3) и найдите его значение при x=0,125.
6*. Вычислите предел последовательности:
а) (n > +?)lim((-4n^3+2n^2-1)/(3n^3+n^2+11)); б) (n > +?)lim((-3n^4+4n)/(2n^3+5n^2+11));
в) (n > +?)lim((2n+1)^(1/3)-(2n)^(1/3)); г) (n > +?)lim(1+3n+5n^2-7n^3).
7*. Четыре ученика, работая совместно с одинаковой производительностью, выполнили задание за некоторый срок. Один мастер и один ученик, работая совместно, выполнили бы это задание за 4/3 того же срока. Во сколько раз производительность мастера больше производительности ученика?
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением






