Упр.868 ГДЗ Мерзляк Полонский 5 класс (Математика)
Решение #1 (Учебник 2024)
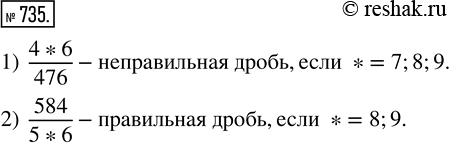
Решение #2 (Учебник 2024)

Решение #3 (Учебник 2019)

Решение #4 (Учебник 2019)




Рассмотрим вариант решения задания из учебника Мерзляк, Полонский, Якир 5 класс, Просвещение:
Какие цифры можно поставить вместо звёздочки, чтобы:
1) дробь 4*6/476 была неправильной;
2) дробь 584/5*6 была правильной?
Дробь, у которой числитель меньше знаменателя, называют правильной.
Дробь, у которой числитель больше знаменателя или равен ему, называют неправильной.
Из двух натуральных чисел с одинаковым количеством цифр больше то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.
1) Для того, чтобы дробь (4*6)/476 была неправильной, надо, чтобы числитель (4*6) был больше или равен знаменателю (476).
Так как у этих чисел совпадают сотни и единицы, достаточно, чтобы в десятках была цифра больше семи (*>7) или равная семи (*=7).
* принимает значения 7, 8, 9.
2) Для того, чтобы дробь 584/(5*6) была правильной, надо, чтобы числитель (584) был меньше знаменателя (5*6).
Так как у этих чисел совпадают сотни, достаточно рассмотреть десятки и единицы.
Если только одна цифра больше восьми – это цифра 9 (9>8, поэтому 596>584).
Если вместо звёздочки поставить цифру 8, то у чисел будут совпадать первые две цифры и надо сравнивать по последней цифре.
6>4, поэтому 586>584.
Таким образом, цифра 8 тоже подходит.
* принимает значения 8, 9.
Решите уравнение:
1) x + 4,83 = 9; 3) x - 14,852 = 15,148
2) 43,78 - x = 5,384; 4) 2,395 + x = 10.
Для того, чтобы из одной десятичной дроби вычесть другую, необходимо:
1) уравнять в уменьшаемом и вычитаемом количество цифр после запятой;
2) записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
3) произвести вычитание так, как вычитают натуральные числа;
4) поставить в полученной разности запятую под запятыми в уменьшаемом и вычитаемом.
Для того, чтобы сложить две десятичные дроби, необходимо:
1) уравнять в слагаемых количество цифр после запятой;
2) записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом второго слагаемого;
3) сложить полученные числа так, как складываются натуральные числа;
4) поставить в полученной сумме запятую под запятыми в слагаемых.
Если к десятичной дроби справа приписать любое количество нулей, то получится дробь, равная данной.
Значение дроби, оканчивающейся нулями, не изменится, если последние нули в её записи отбросить.
1) x+4,83=9
x – неизвестное слагаемое.
Для того, чтобы его найти, необходимо из суммы (9) вычесть известное слагаемое (4,83).
x=9-4,83
x=4,17
У десятичных дробей 4,83 и 9 разное количество цифр после запятой.
Сначала необходимо уравнять количество цифр после запятой.
Допишем справа два нуля к десятичной дроби 9.
9=9,00.
2) 43,78-x=5,384
x – неизвестное вычитаемое.
Для того, чтобы его найти, необходимо из уменьшаемого (43,78) вычесть разность (5,384).
x=43,78-5,384
x=38,396
У десятичных дробей 43,78 и 5,384 разное количество цифр после запятой.
Сначала необходимо уравнять количество цифр после запятой.
Допишем справа один 0 к десятичной дроби 43,78.
43,78=43,780.
3) x-14,852=15,148
x – неизвестное уменьшаемое.
Для того, чтобы его найти, необходимо к разности (15,148) прибавить вычитаемое (14,852).
x=15,148+14,852
x=30
4) 2,395+x=10
x – неизвестное слагаемое.
Для того, чтобы его найти, необходимо из суммы (10) вычесть известное слагаемое (2,395).
x=10-2,395
x=7,605
У десятичных дробей 10 и 2,395 разное количество цифр после запятой.
Сначала необходимо уравнять количество цифр после запятой.
Допишем справа три нуля к десятичной дроби 10.
10=10,000
Похожие решебники
Популярные решебники 5 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







