Упр.7.31 ГДЗ Никольский Потапов 11 класс (Алгебра)
Решение #1
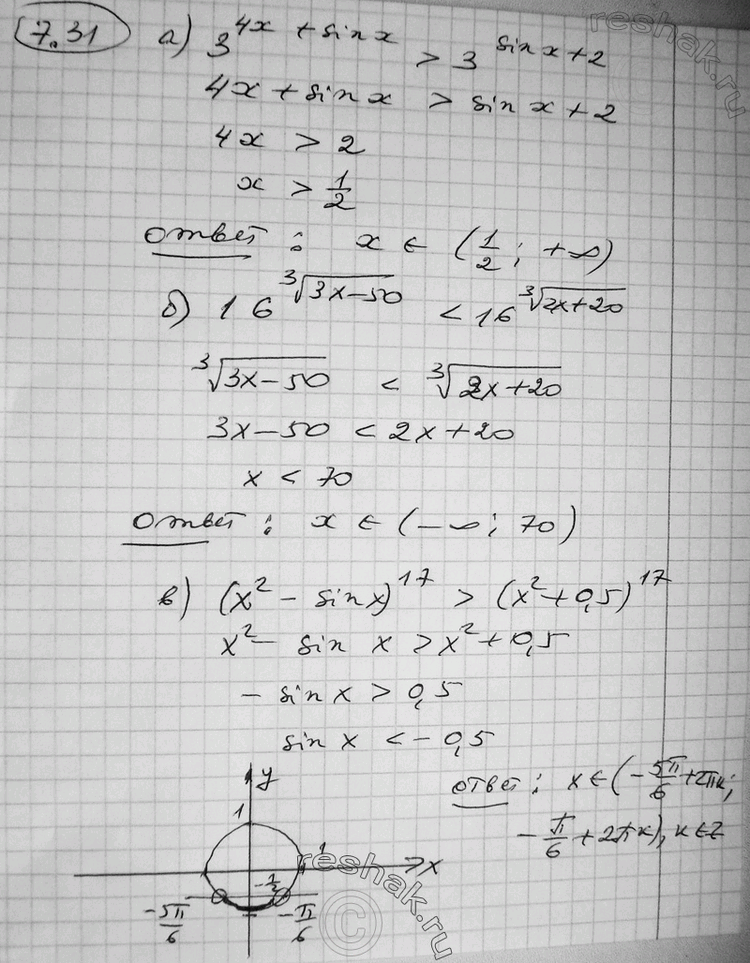
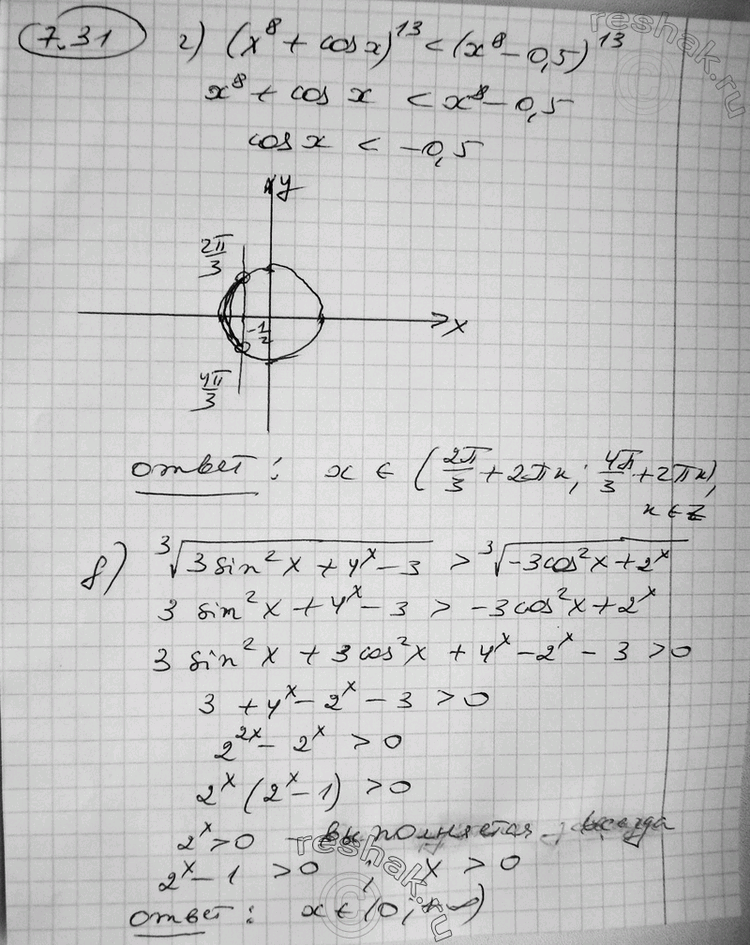
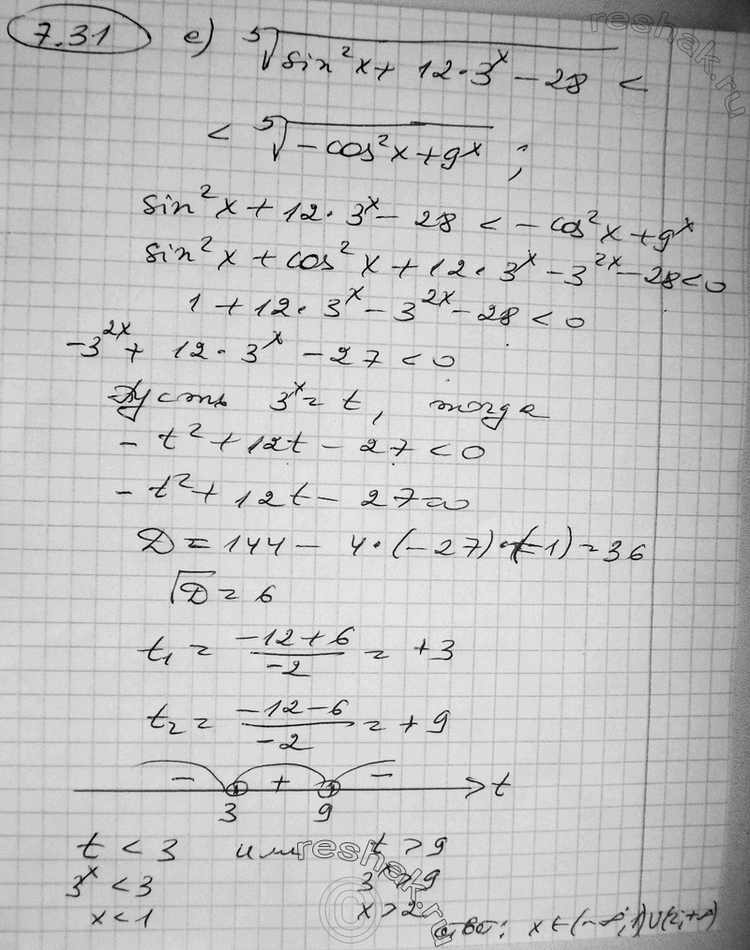
Рассмотрим вариант решения задания из учебника Никольский, Потапов 11 класс, Просвещение:
7.31* а) 3^(4x + sinx) > 3^(sinx + 2);
б) 16^(корень 3 степени (3x-50)) < 16^(корень 3 степени (2x+20));
в) (х2 - sinx)17 > (х2 + 0,5)17;
г) (х8 + cos х)13 < (х8 - 0,5)13;
д) корень 3 степени (3sin2 х + 4х - 3) > корень 3 степени (-3cos2 х + 2х);
е) корень 5 степени (sin2 х + 12 * 3х — 28) < корень 5 степени (-cos2 х + 9x).
Популярные решебники 11 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением