Упр.6.2 ГДЗ Никольский Потапов 11 класс (Алгебра)
Решение #1
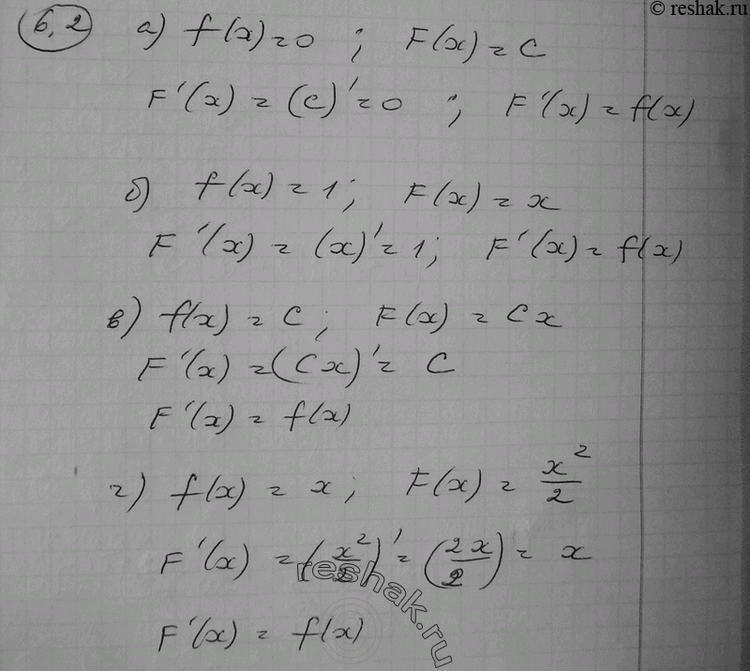
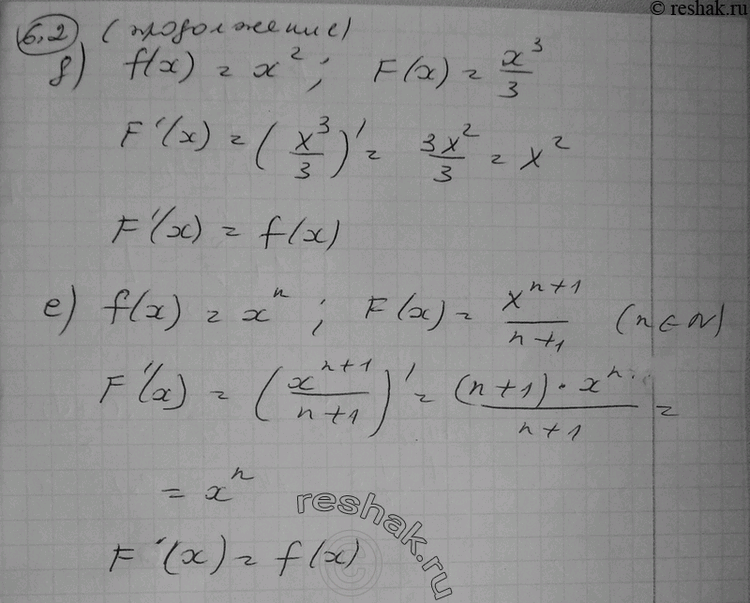
Рассмотрим вариант решения задания из учебника Никольский, Потапов 11 класс, Просвещение:
Докажите, что функция F(x) есть первообразная для функции f(x), если (6.2—6.3):
6.2 а) f(x) = 0, F(x) = С;
б) f(x) = 1, F(x) = х;
в) f(x) = С, F(x) = Сх;
г) f(x) = x,F(x) = x2/2;
д) f(x) = х2, F(x) = x3/3;
е) f(x) = хn, F(x) = x^(n+1)/(n+1) (n принадлежит N).
Популярные решебники 11 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением