Упр.4.71 ГДЗ Виленкин Жохов 5 класс Часть 1, Просвещение (Математика)
Решение #1
Решение #2
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Александрова 5 класс, Просвещение:
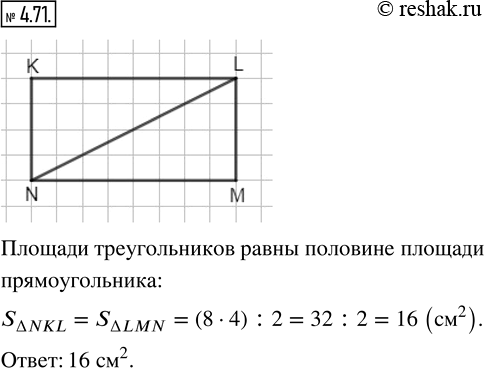
4.71. Начертите прямоугольник KLMN, соедините отрезком вершины L и N. Найдите площади треугольников NKL и LMN, если KL = 8 см и LM = 4 см.
Площадь прямоугольника равна произведению его соседних сторон (длины и ширины).
Тогда, площадь прямоугольника KLMN со сторонами
KL=8 см и LM=4 см равна:
8•4=32 (см^2).
Отрезок LN – диагональ прямоугольника KLMN, а каждая диагональ прямоугольника делит этот прямоугольник на два равных треугольника, то есть треугольники NKL и LMN равны.
Равные фигуры имеют равные площади, значит, площади треугольников NKL и LMN будут равны.
Тогда, площадь каждого из треугольников NKL и LMN равна половине площади прямоугольника KLMN, то есть
32:2=16 (см^2).
Ответ: 16 см^2.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
