Упр.3.238 ГДЗ Виленкин Жохов 5 класс Часть 1, Просвещение (Математика)
Решение #1
Решение #2
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Александрова 5 класс, Просвещение:
3.238. Найдите корень уравнения:
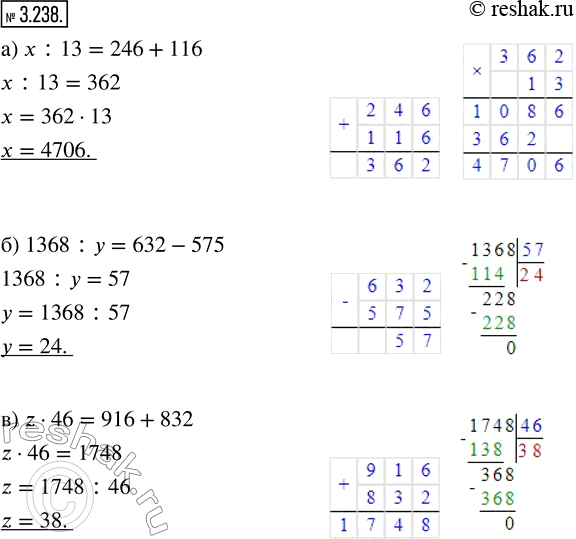
а) x : 13 = 246 + 116; г) (3705 + p) : 59 = 63;
б) 1368 : y = 632 - 575; д) 936 : (124 - k) = 8;
в) z · 46 = 916 + 832; е) (150 - m) · 33 = 1683.
В равенстве a+b=c числа a и b называют слагаемыми, число c и запись a+b – суммой.
В равенстве a-b=c число a называют уменьшаемым, число b – вычитаемым, число c и запись a-b – разностью.
В равенстве a•b=c числа a и b называют множителями, число c и запись a•b – произведением.
В равенстве a:b=c число a называют делимым, число b - делителем, число c и запись a:b – частным.
Уравнение – это равенство, содержащее букву, значение которой необходимо найти.
Корень уравнения – это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
Корень уравнения – это решение уравнения.
Уравнение может иметь один и более корней или не иметь их вообще.
Тогда, говорят, что решить уравнение – значит найти все его корни или показать, что их нет вообще.
а) x:13=246+116
Для начала выполним сложение в правой части выражения.
x:13=362
Теперь решим уравнение относительно деления, то есть неизвестно делимое x.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим:
x=362•13
Или, выполнив умножение:
x=4 706
б) 1 368:y=632-575
Для начала выполним вычитание в правой части выражения.
1 368:y=57
Теперь решим уравнение относительно деления, то есть неизвестен делитель y.
Для того, чтобы найти неизвестный делитель, необходимо делимое разделить на частное, получим:
y=1 368:57
Или, выполнив деление:
y=24
в) z•46=916+832
Для начала выполним сложение в правой части выражения.
z•46=1 748
Теперь решим уравнение относительно умножения, то есть неизвестен множитель z.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим:
z=1 748:46
Или, выполнив деление:
z=38
г) (3 705+p):59=63
Решим уравнение относительно деления, то есть неизвестно делимое 3 705+p.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим:
3 705+p=63•59
Или, выполнив умножение:
3 705+p=3 717
Теперь решаем уравнение относительно сложения, то есть неизвестно слагаемое p.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим:
p=3 717-3 705
Или, выполнив вычитание:
p=12
д) 936:(124-k)=8
Решаем уравнение относительно деления, то есть неизвестен делитель 124-k.
Для того, чтобы найти неизвестный делитель, необходимо делимое разделить на частное, получим:
124-k=936:8
Или, выполнив деление:
124-k=117
Теперь решаем уравнение относительно вычитания, то есть неизвестно вычитаемое k.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разницу, получим:
k=124-117
Или, выполнив вычитание:
k=7
е) (150-m)•33=1683
Решаем уравнение относительно умножения, то есть неизвестен множитель 150-m.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим:
150-m=1 683:33
Или, выполнив деление:
150-m=51
Теперь решаем уравнение относительно вычитания, то есть неизвестно вычитаемое m.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разницу, получим:
m=150-51
Или, выполнив вычитание:
m=99
Похожие решебники
Популярные решебники 5 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением