Упр.1032 ГДЗ Мерзляк Полонский 6 класс (Математика)
Решение #1
Решение #2
Рассмотрим вариант решения задания из учебника Мерзляк, Полонский, Якир 6 класс, Вентана-Граф:
1032. Докажите, что в любой компании из шести человек найдётся трое попарно знакомых или трое попарно незнакомых.
Рассмотрим одного из людей в этой компании. Пусть это будет мистер X, у него есть пять потенциальных знакомых: A,B,C,D и E.
С кем-то он может быть знаком, а с кем-то нет. Может быть знаком и со всеми пятью людьми в компании, а может и наоборот. Все возможные случаи запишем в таблицу.
Получается, что мы всегда можем найти в компании из шести человек трёх знакомых с мистером X или трёх незнакомых с ним людей (что получается и по принципу Дирихле). Рассмотрим каждый из этих случаев.
Знакомство будем рисовать красной линией, а незнакомство – синей.
1) Пусть мистер X знаком хотя бы с тремя людьми из компании. Это могут быть любые из пяти оставшихся человек, например.
Если окажется, что A и C знакомы, или A и E знакомы, или C и E знакомы.
в любом случае мы получим трёх попарно знакомых людей в компании.
Если же окажется, что ни одна из пар A и C, A и E, C и E не знакомы друг с другом:
сразу сможем найти трёх попарно незнакомых друг с другом людей в этой компании.
Таким образом, если случайно выбранный человек имеет хотя бы трёх знакомых в компании, то всегда можно найти трёх попарно знакомых или трёх попарно незнакомых людей в компании из шести человек.
2) Если же мистер X не имеет хотя бы трёх знакомых в этой компании, то мы сможем найти хотя бы трёх незнакомых ему людей.
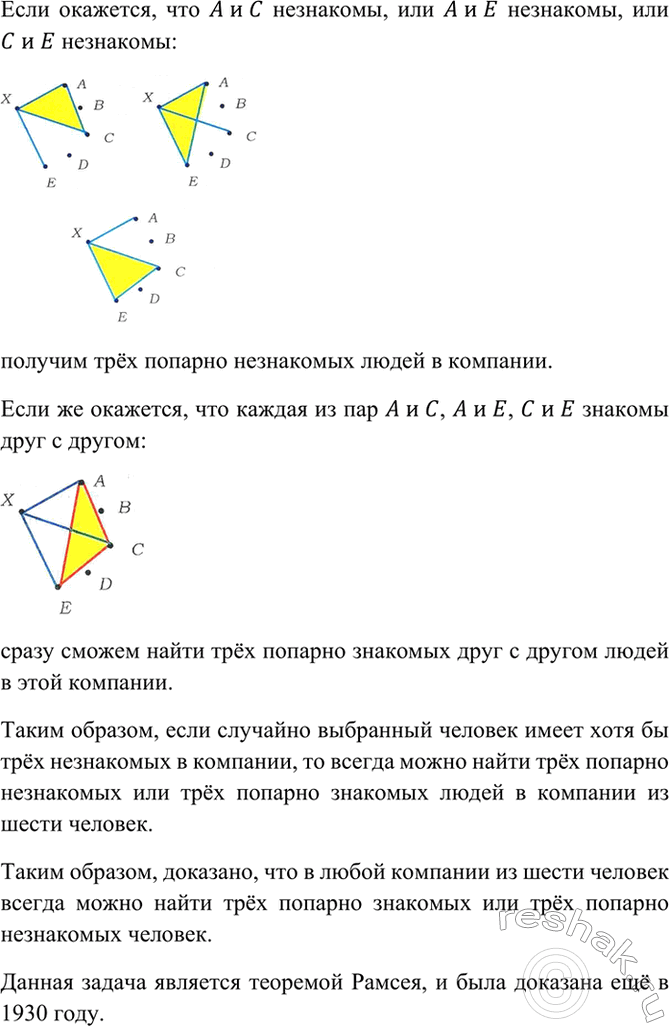
Если окажется, что A и C незнакомы, или A и E незнакомы, или C и E незнакомы.
получим трёх попарно незнакомых людей в компании.
Если же окажется, что каждая из пар A и C, A и E, C и E знакомы друг с другом.
сразу сможем найти трёх попарно знакомых друг с другом людей в этой компании.
Таким образом, если случайно выбранный человек имеет хотя бы трёх незнакомых в компании, то всегда можно найти трёх попарно незнакомых или трёх попарно знакомых людей в компании из шести человек.
Таким образом, доказано, что в любой компании из шести человек всегда можно найти трёх попарно знакомых или трёх попарно незнакомых человек.
Данная задача является теоремой Рамсея, и была доказана ещё в 1930 году.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
