Упр.42.26 ГДЗ Мордковича 10 класс профильный уровень (Алгебра)
Решение #1
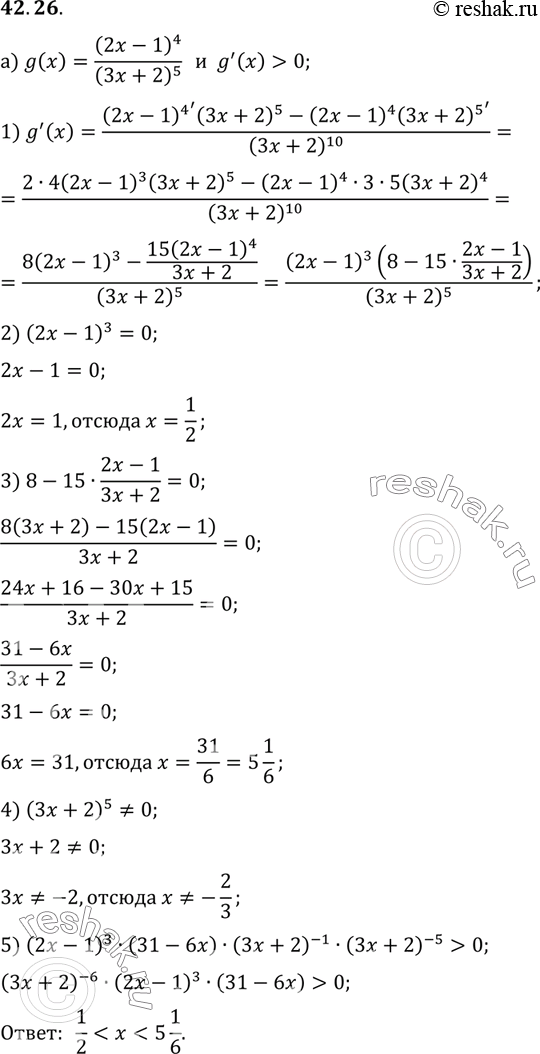
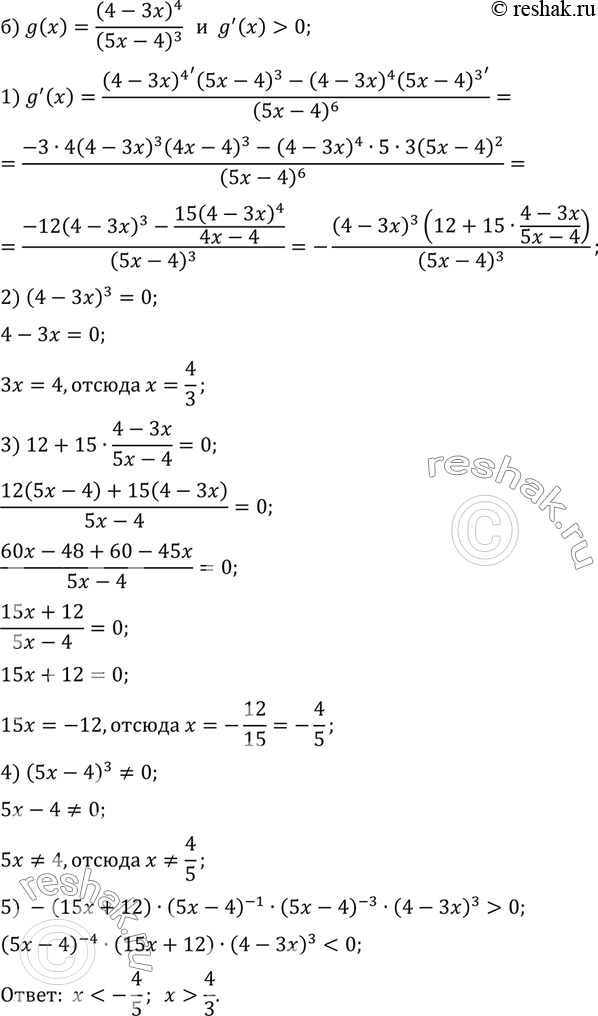
Решение #2(записки учителя)
Решение #3(записки школьника)
Рассмотрим вариант решения задания из учебника
Мордкович, Семенов 10 класс, Мнемозина:
Решите неравенство g'(x) > 0, если:
a) g(x) = ((2x - 1)4)/((3x + 2)5);
б) g(x) = ((4 - 3x)4)/((5x - 4)3).
