Упр.42.20 ГДЗ Мордковича 10 класс профильный уровень (Алгебра)
Решение #1
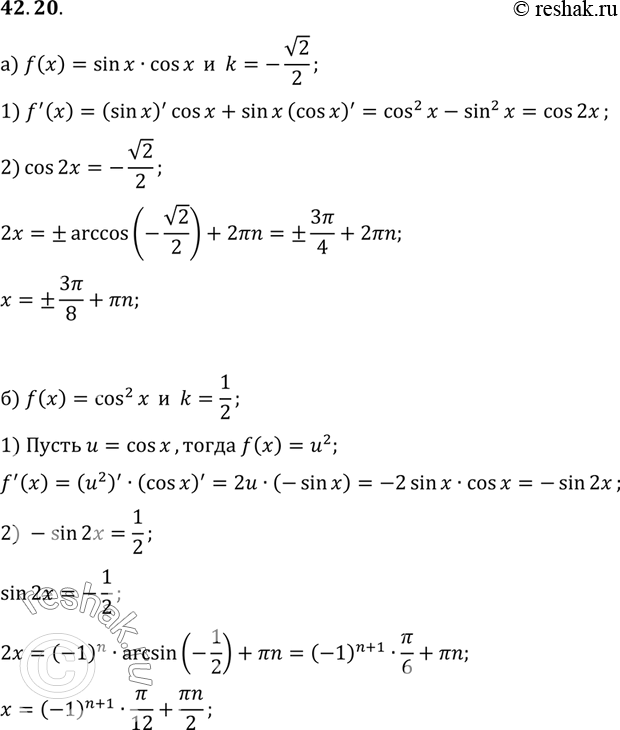
Решение #2(записки учителя)
Решение #3(записки школьника)
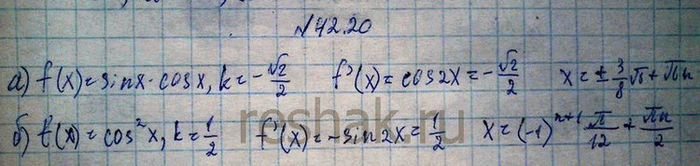
Рассмотрим вариант решения задания из учебника Мордкович, Семенов 10 класс, Мнемозина:
Определите абсциссы точек, в которых угловой коэффициент касательной к графику функции у = f(x) равен а, если:
a) f(x) = sin x cos x, k = -корень2 / 2;
б) f(x) = cos2 x, k = 1/2.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
