Упр.588 ГДЗ Макарычев Миндюк 9 класс (Алгебра)
Решение #1 (Учебник 2026)
Решение #2 (Учебник 2026)
Решение #3 (Учебник 2026)
Решение #4 (Учебник 2024)
Решение #5 (Учебник 2024)
Решение #6 (Учебник 2024)
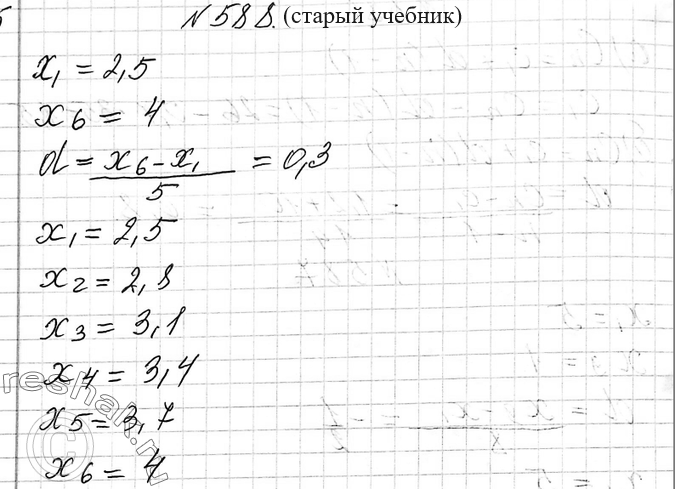
Решение #7 (Учебник 2024)
Рассмотрим вариант решения задания из учебника
Макарычев, Миндюк, Нешков 9 класс, Просвещение:
Задание учебника 2026 года
Покажите штриховкой множество точек, которое задаёт на координатной плоскости система неравенств
система
у > = х2,
2у + х < = 5.
Задание учебника 2024 года
(Задача-исследование.) Могут ли числа 20 и 35 быть членами арифметической прогрессии, первый член которой равен 12 и разность не равна 1.
1) Предположив, что числа 20 и 35 являются членами арифметической прогрессии, выразите каждое из них через d, n или m, где d — разность прогрессии, n — номер члена, равного 20, m — номер члена, равного 35. Докажите, что n-1/m-1 = 8/23
2) Полагая, что n-1 = 8k и m-1=23k, где k принадлежит N, выразите тип через k. Обсудите, как, выбрав значение k, большее 1, можно получить арифметическую прогрессию, удовлетворяющую условию задачи. Выполните необходимые вычисления.
3) Объясните, почему значение k = 1 приводит к противоречию с условием задачи.
