Упр.1365 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 9 класс, Просвещение:
1365. Дана окружность О радиуса r и точка А плоскости. Докажите, что множество середин отрезков АМ, где М — любая точка окружности О радиуса r, есть окружность. Укажите положение центра этой окружности и найдите её радиус.
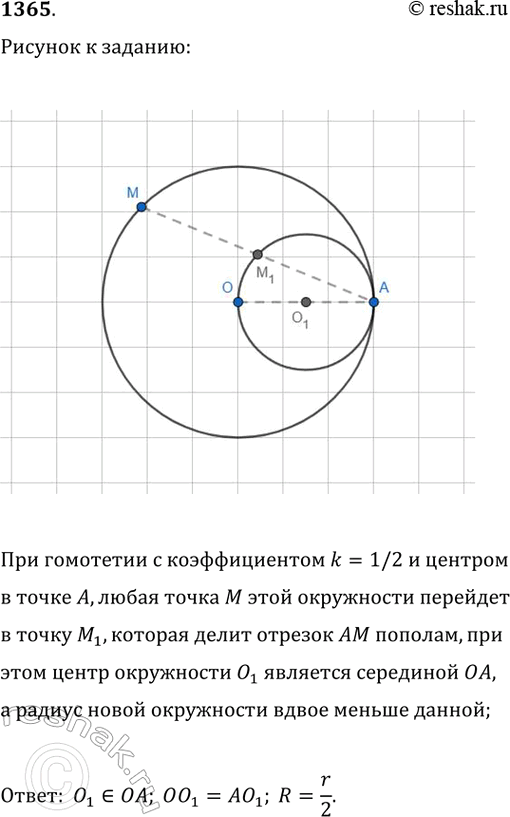
При гомотетии с коэффициентом k=1/2 и центром в точке A, любая точка M этой окружности перейдет в точку M_1,которая делит отрезок AM пополам, при этом центр окружности O_1 является серединой OA, а радиус новой окружности вдвое меньше данной;
Ответ: O_1 принадлежит OA; OO_1=AO_1; R=r/2.
Похожие решебники
Популярные решебники 9 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







