Упр.792 ГДЗ Макарычев 7 класс (Алгебра)
Решение #1
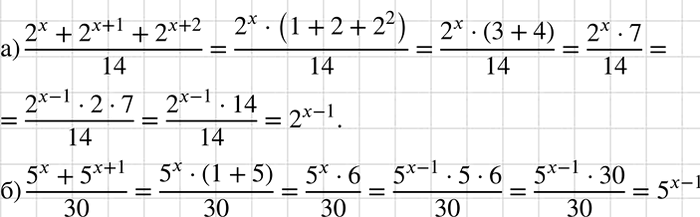
Решение #2
Рассмотрим вариант решения задания из учебника Макарычев, Миндюк 7 класс, Просвещение:
Докажите, что:
а) сумма трёх последовательных степеней числа 2 с натуральными показателями делится на 14;
б) сумма двух последовательных степеней числа 5 с натуральными показателями делится на 30.
а) Пусть три последовательных степени числа 2 будут: 2^n,2^(n+1),2^(n+2).
Докажем, что сумма трёх последовательных степеней числа 2 с натуральными показателями делится на 14.
2^n+2^(n+1)+2^(n+2)=2^n (1+2+2^2 )=2^n•7=2^(n-1)•2•7==2^(n-1)•14
Так как один из множителей число 14, то выражение делится на 14, при n?1.
Что и требовалось доказать.
б) Пусть две последовательные степени числа 5 будут: 5^n,5^(n+1).
Докажем, что сумма двух последовательных степеней числа 5 с натуральными показателями делится на 30.
5^n+5^(n+1)=5^n (1+5)=5^n•6=5^(n-1)•5•6=5^(n-1)•30
Так как один из множителей число 30, то выражение делится на 30, при n?1.
Что и требовалось доказать.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
