Стр.84 Часть 2 ГДЗ Дорофеев Миракова 4 класс (Математика)
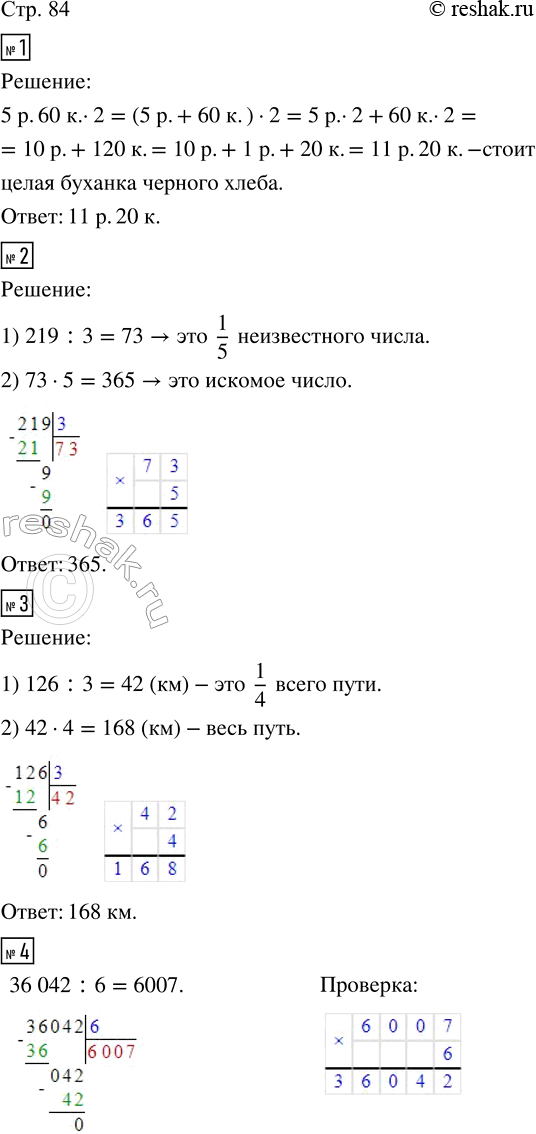
Решение #1


Решение #2














Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
1. Половина буханки чёрного хлеба стоит 5 р. 60 к. Сколько стоит целая буханка?
2. Три пятых неизвестного числа равны 219. Найди это число.
3. Автомобиль проехал 3/4 пути, что составляет 126 км. Найди длину всего пути.
4. Выполни деление и сделай проверку.
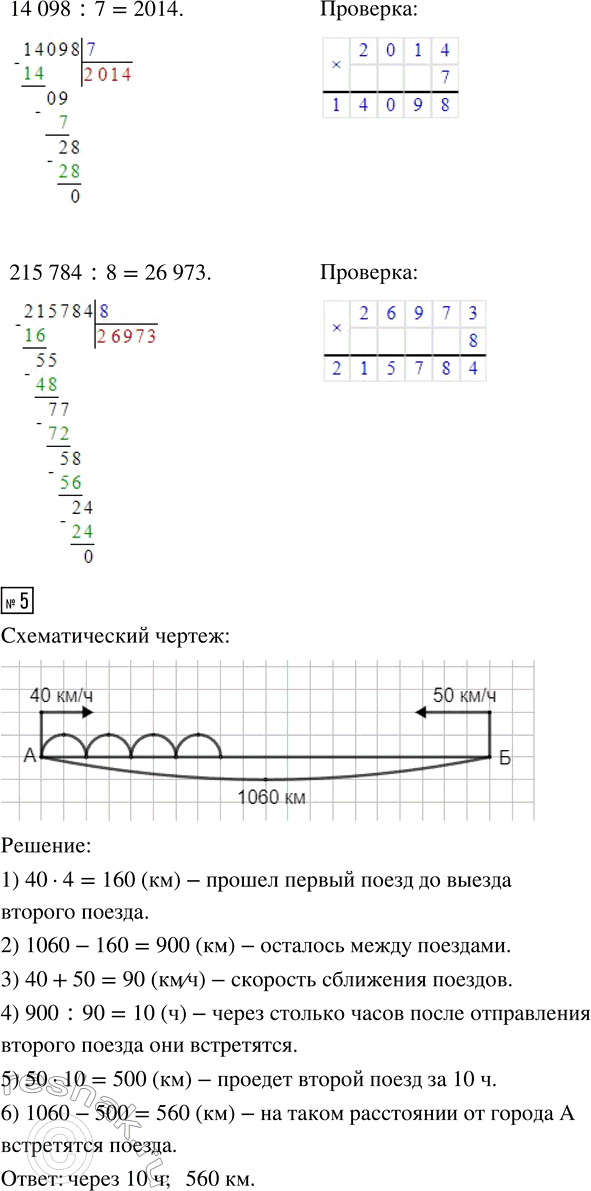
36 042 : 6 14 098 : 7 215 784 : 8
5. Расстояние между городами А и Б равно 1 060 км. Из города А отправился поезд со скоростью 40 км/ч, а через 4 ч навстречу ему отправился поезд из города Б со скоростью 50 км/ч. Через сколько часов после отправления второго поезда и на каком расстоянии от города А встретятся эти поезда?
Схематический чертёж поможет тебе решить задачу.
6. Вычисли значения выражений.
25 011 · (255 : 5 · 34 - 15 579 : 9) + 7 533
(783 512 - 11 399 · 64) : 6 + 1 004
7. Который сейчас час, если прошедшая часть суток на 6 ч 27 мин больше оставшейся?
8. Сравни.
5 т 605 кг и 5 650 кг 12 км 58 м и 12 058 м
40 ц 42 кг и 4 т 420 кг 8 ч 12 мин и 490 мин
9. Мотоциклист должен был проехать расстояние между двумя пунктами, равное 90 км, со скоростью 30 км/ч, но в дороге он вынужден был задержаться на 1 ч. Чтобы прибыть вовремя на место назначения, он после остановки увеличил свою скорость в 2 раза. На каком расстоянии от начала движения произошла остановка?
2.
Три пятых числа в 3 раза больше одной пятой числа, значит, необходимо три пятых числа разделить на 3.
Запишем одну пятую числа.
219 3
21 73
9
9
0
Пишем: 219:3.
Первое неполное делимое – 21 десяток. Значит, в частном будет 2 цифры.
Делю десятки: разделю 21 на 3, получу 7 - столько десятков будет в частном.
Умножу 3 на 7, получу 21 - столько десятков разделили.
Вычту: 21-21=0 – десятки разделили все.
Делю единицы: разделю 9 на 3, получу 3 - столько единиц будет в частном.
Умножу 3 на 3, получу 9 - столько единиц разделили.
Вычту: 9-9=0 – единицы разделили все.
Читаю ответ: 73.
Значит, одна пятая числа равна 73.
В числе содержится 5 раз по одной пятой, значит, необходимо одну пятую умножить на 5.
73
5
365
Пишу: 73•5.
Умножаю единицы: 3•5=15. 15 ед. – это 1 дес. 5 единиц; пишу 5 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Умножаю десятки: 7•5=35, да ещё 1.
35+1=36. 36 дес. – это 3 сот. 6 дес.; пишу 6 под дес., а 3 сотни пишу под сотнями, так как других сотен для умножения нет.
Читаю ответ: 365.
Значит, искомое число равно 365.
3.
Запишем условие задачи.
3/4 пути - 126 км
Весь путь - ? км
3/4 пути в 3 раза больше 1/4 пути, значит, необходимо 3/4 пути разделить на 3.
Запишем 1/4 пути.
126 3
12 42
6
6
0
Пишем: 126:3.
Первое неполное делимое – 12 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 12 на 3, получу 4 - столько десятков будет в частном.
Умножу 3 на 4, получу 12 - столько десятков разделили.
Вычту: 12-12=0 – десятки разделили все.
Делю единицы: разделю 6 на 3, получу 2 - столько единиц будет в частном.
Умножу 3 на 2, получу 6 - столько единиц разделили.
Вычту: 6-6=0 – единицы разделили все.
Читаю ответ: 42.
Значит, 1/4 пути равна 42.
Во всём пути содержится 4 раза по 1/4 пути, значит, необходимо 1/4 пути умножить на 4.
42•4=168
Значит, длина всего пути равна 168 км.
4.
Для того, чтобы проверить правильно ли выполнено деление, необходимо частное умножить на делитель, и, если в результате получится делимое, то деление выполнено верно.
36042 6
36 6007
42
42
0
Пишем: 36 042:6.
Первое неполное делимое – 36 тысяч. Значит, в частном будет 4 цифры.
Делю тысячи: разделю 36 на 6, получу 6 - столько тысяч будет в частном.
Умножу 6 на 6, получу 36 - столько тысяч разделили.
Вычту: 36-36=0 – тысячи разделили все.
Делю сотни: 0 сотен нельзя разделить на 6 так, чтобы в частном получились сотни, поэтому пишем в частном 0.
Делю десятки: 4 десятка нельзя разделить на 6 так, чтобы в частном получились десятки, поэтому пишем в частном 0.
Делю единицы: 4 десятка 2 единицы – это 42 единицы.
Разделю 42 на 6, получу 7 - столько единиц будет в частном.
Умножу 6 на 7, получу 42 - столько единиц разделили.
Вычту: 42-42=0 – единицы разделили все.
Читаю ответ: 6 007.
Проверка:
6007
6
36042
Пишу: 6 007•6.
Умножаю единицы: 7•6=42. 42 ед. – это 4 дес. 2 ед.; пишу 2 под единицами, а 4 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 0•6=0, да ещё 4.
0+4=4. Пишу 4 под десятками.
Умножаю сотни: 0•6=0. Пишу 0 под сотнями.
Умножаю единицы тысяч: 6•6=36. 36 ед. тыс. – это 3 дес. тыс. 6 ед. тыс.; пишу 6 под ед. тыс., а 3 дес. тысяч пишу под десятками тысяч, так как других десятков тысяч для умножения нет.
Читаю ответ: 36 042.
Значит, деление выполнено верно.
14098 7
14 2014
9
7
28
28
0
Пишем: 14 098:7.
Первое неполное делимое – 14 тысяч. Значит, в частном будет 4 цифры.
Делю тысячи: разделю 14 на 7, получу 2 - столько тысяч будет в частном.
Умножу 7 на 2, получу 14 - столько тысяч разделили.
Вычту: 14-14=0 – тысячи разделили все.
Делю сотни: 0 сотен нельзя разделить на 7 так, чтобы в частном получились сотни, поэтому пишем в частном 0.
Делю десятки: разделю 9 на 7, получу 1 – столько десятков будет в частном.
Умножу 7 на 1, получу 7 - столько десятков разделили.
Вычту: 9-7=2 – столько десятков осталось разделить.
Делю единицы: 2 десятка 8 единиц – это 28 единиц. Разделю 28 на 7, получу 4 - столько единиц будет в частном.
Умножу 7 на 4, получу 28 - столько единиц разделили.
Вычту: 28-28=0 – единицы разделили все.
Читаю ответ: 2 014.
Проверка:
2014
7
14098
Пишу: 2 014•7.
Умножаю единицы: 4•7=28. 28 ед. – это 2 дес. 8 ед.; пишу 8 под единицами, а 2 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 1•7=7, да ещё 2.
7+2=9. Пишу 9 под десятками.
Умножаю сотни: 0•7=0. Пишу 0 под сотнями.
Умножаю единицы тысяч: 2•7=14. 14 ед. тыс. – это 1 дес. тыс. 4 ед. тыс.; пишу 4 под ед. тыс., а 1 дес. тысяч пишу под десятками тысяч, так как других десятков тысяч для умножения нет.
Читаю ответ: 14 098.
Значит, деление выполнено верно.
215784 8
16 26973
55
48
77
72
58
56
24
24
0
Пишем: 215 784:8.
Первое неполное делимое – 21 десяток тысяч. Значит, в частном будет 5 цифр.
Делю десятки тысяч: разделю 21 на 8, получу 2 - столько десятков тысяч будет в частном.
Умножу 8 на 2, получу 16 - столько десятков тысяч разделили.
Вычту: 21-16=5 – столько дес. тысяч осталось разделить.
Делю единицы тысяч: 5 десятков тысяч 5 единиц тысяч – это 55 единиц тысяч.
Разделю 55 на 8, получу 6 - столько ед. тысяч будет в частном.
Умножу 8 на 6, получу 48 - столько единиц тысяч разделили.
Вычту: 55-48=7 – столько единиц тысяч осталось разделить.
Делю сотни: 7 единиц тысяч 7 сотен – это 77 сотен.
Разделю 77 на 8, получу 9 - столько сотен будет в частном.
Умножу 8 на 9, получу 72 - столько сотен разделили.
Вычту: 77-72=5 – столько сотен осталось разделить.
Делю десятки: 5 сотен 8 десятков – это 58 десятков.
Разделю 58 на 8, получу 7 - столько десятков будет в частном.
Умножу 8 на 7, получу 56 - столько десятков разделили.
Вычту: 58-56=2 – столько десятков осталось разделить.
Делю единицы: 2 десятка 4 единицы – это 24 единицы.
Разделю 24 на 8, получу 3 - столько единиц будет в частном.
Умножу 8 на 3, получу 24 - столько единиц разделили.
Вычту: 24-24=0 – единицы разделили все.
Читаю ответ: 26 973.
Проверка:
26 973
8
215 784
Пишу: 26 973•8.
Умножаю единицы: 3•8=24. 24 ед. – это 2 дес. 4 ед.; пишу 4 под единицами, а 2 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 7•8=56, да ещё 2.
56+2=58. 58 десятков – это 5 сотен 8 десятков; пишу 8 под десятками, а 5 сотен запомню и прибавлю к сотням.
Умножаю сотни: 9•8=72, да ещё 5.
72+5=77. 77 сот. – это 7 ед. тыс. 7 сотен; пишу 7 под сотнями, а 7 единиц тысяч запомню и прибавлю к единицам тысяч.
Умножаю единицы тысяч: 6•8=48, да ещё 7.
48+7=55. 55 ед. тыс. – это 5 дес. тыс. 5 ед. тыс.; пишу 5 под ед. тыс., а 5 дес. тысяч запомню и прибавлю к десяткам тысяч.
Умножаю десятки тысяч: 2•8=16, да ещё 5.
16+5=21. 21 десяток тысяч – это 2 сотни тысяч 1 десяток тысяч; пишу 1 под десятками тысяч, а 2 сотни тысяч пишу под сотнями тысяч, так как других сотен тысяч для умножения нет.
Читаю ответ: 215 784.
Значит, деление выполнено верно.
5.
Запишем краткое условие задачи.
Расстояние между городами - 1 060 км
Скорость 1 поезда - 40 км/ч
Скорость 2 поезда - 50 км/ч
2 поезд отправился на 4 часа позже
Поезда встретятся через ? часов и на расстоянии ? км от А
Для того, чтобы найти расстояние по известным скорости и времени, необходимо скорость умножить на время.
Определим, как найти, какое расстояние прошёл первый поезд до момента выхода второго поезда.
Для этого необходимо скорость первого поезда умножить на время его движения, то есть 4 часа.
40•4=160 (км) – прошёл первый поезд до момента выхода второго поезда.
Определим, как найти, какое расстояние было между поездами в момент выхода второго поезда.
Для этого, необходимо из расстояния между городами вычесть расстояние, которое прошёл первый поезд.
1 060-160=900 (км) – было между поездами в момент выхода второго поезда.
Скорость сближения – это величина, на которую уменьшается расстояние между двумя объектами за единицу времени.
Для того, чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, необходимо сложить их скорости.
V_(сбл.)=V_1+V_2
Тогда, V_(сбл.)=40+50=90 (км/ч) – скорость сближения поездов.
Определим, как найти время встречи поездов.
Для этого, необходимо расстояние между поездами разделить на скорость их сближения.
Значит, 900:90=90:9=10 (ч) – время встречи поездов после отправления второго поезда.
Определим, как найти, какое расстояние прошёл первый поезд с момента выхода второго до их встречи.
Для этого, необходимо скорость первого поезда умножить на время их встречи.
40•10=400 (км) – прошёл первый поезд с момента выхода второго поезда до их встречи.
Определим, как найти, какое расстояние прошёл первый поезд от города А до места встречи поездов.
Для этого, необходимо сложит расстояния, которые прошёл первый поезд до момента выхода второго поезда и после.
160+400=560 (км) – прошёл первый поезд о города А до места встречи поездов.
Ответ: через 10 часов; 560 км.
6.
Действия в числовых выражениях выполняются в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
5 1 2 4 3 6
25 011•(255:5•34-15 579:9)+7 533=
=25 011•(51•34-15 579:9)+7 533=
=25 011•(1 734-15 579:9)+7 533=
=25 011•(1 734-1 731)+7 533=25 011•3+7 533=
=75 033+7 533=82 566
51
34
204
153
1734
Пишу: 51•34.
Умножу первый множитель на число единиц: 51•4=204.
Получу первое неполное произведение: 204.
Умножу первый множитель на число десятков: 51•3=153.
Получу второе неполное произведение: 153 десятка.
Начну подписывать второе неполное произведение под десятками. Сложу неполные произведения.
Читаю ответ: 1 734. Это произведение чисел 51 и 34.
15579 9
9 1731
65
63
27
27
9
9
0
Пишем: 15 579:9.
Первое неполное делимое – 15 тысяч. Значит, в частном будет 4 цифры.
Делю тысячи: разделю 15 на 9, получу 1 - столько тысяч будет в частном.
Умножу 9 на 1 , получу 9 - столько тысяч разделили.
Вычту: 15-9=6 – столько тысяч осталось разделить.
Делю сотни: 6 тысяч 5 сотен – это 65 сотен.
Разделю 65 на 9, получу 7 - столько сотен будет в частном.
Умножу 9 на 7, получу 63 - столько сотен разделили.
Вычту: 65-63=2 – столько сотен осталось разделить.
Делю десятки: 2 сотни 7 десятков – это 27 десятков.
Разделю 27 на 9, получу 3 - столько десятков будет в частном.
Умножу 9 на 3, получу 27 - столько десятков разделили.
Вычту: 27-27=0 – десятки разделили все.
Делю единицы: разделю 9 на 9, получу 1 - столько единиц будет в частном.
Умножу 9 на 1, получу 9 - столько единиц разделили.
Вычту: 9-9=0 – единицы разделили все.
Читаю ответ: 1 731.
2 1 3 4
(783 512-11 399•64) :6+1 004=
=(783 512-729 536) :6+1 004=53 976:6+1 004=
=8 996+1 004=10 000
11399
64
45596
68394
729536
Пишу: 11 399•64.
Умножу первый множитель на число единиц:
11 399•4=45 596.
Получу первое неполное произведение: 45 596.
Умножу первый множитель на число десятков:
11 399•6=68 394.
Получу второе неполное произведение: 68 394 десятка.
Начну подписывать второе неполное произведение под десятками. Сложу неполные произведения.
Читаю ответ: 729 536. Это произведение чисел 11 399 и 64.
783 512
729 536
53 976
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч): 783 512-729 536.
Вычитаем единицы: из 2 единиц нельзя вычесть 6 единиц, поэтому возьмём из 1 десятка 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 1). 10+2=12.
Вычтем: 12-6=6. Пишем 6 под единицами.
Вычитаем десятки: был 1 дес., но после того, как заняли 1 дес. при вычитании ед., осталось 0 дес. Из 0 дес. нельзя вычесть 3 дес., поэтому возьмём из 5 сот. 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 5). 10+0=10.
Вычтем: 10-3=7. Пишем 7 под десятками.
Вычитаем сотни: было 5 сотен, но после того, как заняли 1 сотню при вычитании десятков, осталось 4 сотни. Из 4 сотен нельзя вычесть 5 сотен, поэтому возьмём из 3 единиц тысяч 1 тысячу, то есть 10 сотен (для того, чтобы не забыть, поставим точку над цифрой 3). 10+4=14.
Вычтем: 14-5=9. Пишем 9 под сотнями.
Вычитаем единицы тысяч: было 3 ед. тыс., но после того, как заняли 1 ед. тыс. при вычитании сот., осталось 2 ед. тыс. Из 2 ед. тысяч нельзя вычесть 9 единиц тысяч, поэтому возьмём из 8 десятков тысяч 1 десяток тысяч, то есть 10 единиц тысяч (для того, чтобы не забыть, ставим точку над цифрой 8). 10+2=12.
Вычтем: 12-9=3. Пишем 3 под единицами тысяч.
Вычитаем десятки тысяч: было 8 дес. тыс., но после того, как заняли 1 дес. тыс. при вычитании ед. тыс., осталось 7 дес. тысяч.
Вычтем: 7-2=5. Пишем 5 под десятками тысяч.
Вычитаем сотни тысяч: 7-7=0. 0 под высшим разрядом принято не писать.
Читаем ответ: 53 976.
53976 6
48 8996
59
54
57
54
36
36
0
Пишем: 53 976:6.
Первое неполное делимое – 53 тысячи. Значит, в частном будет 4 цифры.
Делю тысячи: разделю 53 на 6, получу 8 - столько тысяч будет в частном.
Умножу 6 на 8 , получу 48 - столько тысяч разделили.
Вычту: 53-48=5 – столько тысяч осталось разделить.
Делю сотни: 5 тысяч 9 сотен – это 59 сотен.
Разделю 59 на 6, получу 9 - столько сотен будет в частном.
Умножу 6 на 9, получу 54 - столько сотен разделили.
Вычту: 59-54=5 – столько сотен осталось разделить.
Делю десятки: 5 сотен 7 десятков – это 57 десятков.
Разделю 57 на 6, получу 9 - столько десятков будет в частном.
Умножу 6 на 9, получу 54 - столько десятков разделили.
Вычту: 57-54=3 – столько десятков осталось разделить.
Делю единицы: 3 десятка 6 единиц – это 36 единиц.
Разделю 36 на 6, получу 6 - столько единиц будет в частном.
Умножу 6 на 6, получу 36 - столько единиц разделили.
Вычту: 36-36=0 – единицы разделили все.
Читаю ответ: 8 996.
7.
Запишем краткое условие задачи.
Прошедшая часть суток - ?, на 6 ч 27 мин больше оставшейся
Сейчас времени - ?
Вспомним перевод мер времени.
1 сутки=24 часа.
1 час=60 минут
Переведём 6 ч 27 мин в минуты.
6 ч 27 мин=6 ч+27 мин=6•1 ч+27 мин=
=6•60 мин+27 мин=360 мин+27 мин=387 мин.
Переведём 1 сутки в минуты.
1 сутки=24 ч=24•1 ч=24•60 мин=1 440 мин.
Пусть x - оставшаяся часть суток.
Тогда, x+387 – прошедшая часть суток.
Сутки складываются из прошедшей и оставшейся частей, значит, x+x+387=1 440
Приведём подобные слагаемые: 2x+387=1 440.
Если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
Перенесём 387 в правую часть уравнения.
2x=1 440-387
1 440
387
1 053
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 1 440-387.
Вычитаем единицы: из 0 единиц нельзя вычесть 7 единиц, поэтому возьмём из 4 десятков 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 4). 10+0=10.
Вычтем: 10-7=3. Пишем 3 под единицами.
Вычитаем десятки: было 4 дес., но после того, как заняли 1 дес. при вычитании ед., осталось 3 дес. Из 3 дес. нельзя вычесть 8 дес., поэтому возьмём из 4 сот. 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 4). 10+3=13.
Вычтем: 13-8=5. Пишем 5 под десятками.
Вычитаем сотни: было 4 сот., но после того, как заняли 1 сот. при вычитании дес., осталось 3 сот. 3-3=0. Пишем 0 под сотнями.
Спускаем в ответ 1 тысячу.
Читаем ответ: 1 053.
2x=1 053
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
Разделим обе части уравнения на 2, получим x=1053/2 .
x=526 1/2 мин=526 мин 30 с - оставшаяся часть суток.
Найдём прошедшую часть суток.
526 мин 30 с+387 мин=(526 мин+30 с)+387 мин=
=526 мин+30 с+387 мин=(526 мин+387 мин)+30 с=
=913 мин+30 с=913 мин 30 с.
Переведём 913 мин 30 с в часы, минуты и секунды.
913 мин 30 с=913 мин+30 с=900 мин+13 мин+30 с=
=15•60 мин+13 мин+30 с=15•1 ч+13 мин+30 с=
=15 ч+13 мин+30 с=15 ч 13 мин 30 с.
Ответ: 15 ч 30 мин 30 с.
8.
Вспомним о том, что 1 т=1 000 кг, тогда
5 т 605 кг=5 т+605 кг=5•1 т+605 кг=
=5•1 000 кг+605 кг=5 000 кг+605 кг=5 605 кг.
5 605 кг < 5 650 кг, значит и 5 т 605 кг < 5 650 кг.
Вспомним о том, что 1 т=10 ц, тогда
4 т 420 кг=4 т+420 кг=4•1 т+420 кг=
=4•10 ц+420 кг=40 ц+420 кг=40 ц 420 кг.
40 ц 42 кг < 40 ц 420 кг, значит и 40 ц 42кг < 4 т 420 кг.
Вспомним о том, что 1 км=1 000 м, тогда
12 км 58 м=12 км+58 м=12•1 км+58 м=
=12•1 000 м+58 м=12 000 м+58 м=12 058 м.
12 058 м=12 058 м, значит и 12 км 58 м=12 058 м.
Вспомним о том, что 1 ч=60 мин, тогда
8 ч 12 мин=8 ч+12 мин=8•1 ч+12 мин=
=8•60 мин+12 мин=480 мин+12 мин=492 мин.
492 мин > 490 мин, значит и 8 ч 12 мин > 490 мин.
9.
Определим, как найти время, за которое мотоциклист должен был проделать путь.
Для этого, необходимо весь путь разделить на скорость мотоциклиста.
90:30=3 (ч) – затратил мотоциклист на весь путь.
Определим, сколько времени мотоциклист ехал.
Для этого, необходимо из времени всего движения вычесть время остановки.
3-1=2 (ч) – мотоциклист ехал.
Для того, чтобы найти расстояние по известным скорости и времени, необходимо скорость умножить на время.
Сравним ожидаемое и фактическое движение мотоциклиста.
Ожидаемое движение – движение, если бы мотоциклист не остановился, то есть планируемое.
Фактическое движение – движение мотоциклиста с вынужденной остановкой.
В обоих случаях мотоциклист сначала сколько-то ехал со скоростью 30 км/ч.
Затем во втором случае он сделал остановку на 1 час, а в первом – продолжил движение со скоростью 30 км/ч и проехал
30•1=30 км.
Получилось, что в первом случае он проехал на 30 км больше к этому моменту.
Затем в первом случае мотоциклист продолжил движение до второго пункта со скоростью 30 км/ч, а во втором случае – со скоростью 60 км/ч.
Причём, во втором случае мотоциклист проехал на 30 км больше, чем в первом, потому что в начале этого отрезка от отставал на 30 км, а в конце отрезка он в обоих случаях достиг места назначения.
Найдём, сколько времени длился последний отрезок пути.
Скорость мотоциклиста во втором случае в 2 раза больше, чем в первом, а время движения одинаковое. Значит, во втором случае мотоциклист проехал в 2 раза больше, чем в первом, то есть пройденное во втором случае расстояние складывается из двух расстояний, пройденных в первом случае.
Известно, что во втором случае он проехал на 30 км больше, чем в первом, что и будет являться расстоянием, пройденным в первом случае.
Для того, чтобы найти время, необходимо расстояние разделить на скорость: 30:30=1 (ч) – время движения после остановки.
Найдём время движения до остановки.
Для этого из всего времени движения вычтем время движения после остановки.
2-1=1 (ч) – время движения до остановки.
Найдём, на каком расстоянии от начала движения произошла остановка.
Для этого, необходимо скорость умножить на время движения.
30•1=30 (км) – расстояние от начала движения, на котором произошла остановка.
Ответ: 30 км.
Похожие решебники
Популярные решебники 4 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.