Упр.676 ГДЗ Никольский Потапов 5 класс (Математика)
Решение #1
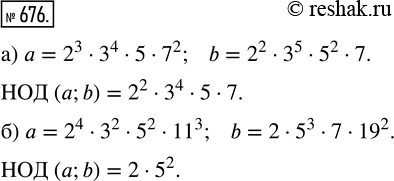
Рассмотрим вариант решения задания из учебника Никольский, Потапов, Решетников 5 класс, Просвещение:
676. Даны разложения чисел а и b на простые множители. Найдите НОД (а, b).
а) а = 2^3 · 3^4 · 5 · 7^2, б) а = 2^4 · 3^2 · 5^2 · 11^3,
b = 2^2 · 3^5 · 5^2 · 7; b = 2 · 5^3 · 7 · 19^2.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
