Упр.4.71 ГДЗ Никольский Потапов 11 класс (Алгебра)
Решение #1
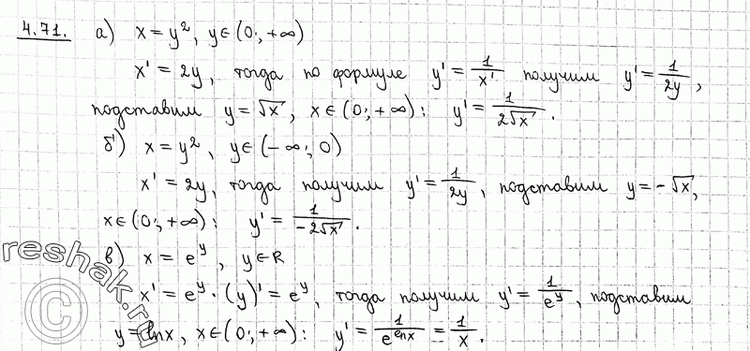
Решение #2
Рассмотрим вариант решения задания из учебника Никольский, Потапов 11 класс, Просвещение:
4.71 Вычислите производную функции у = f(х), используя производную обратной к ней функции х = фи (y):
а) у = корень х, х принадлежит (0; +бесконечность) и х = y2, у принадлежит (0; +бесконечность);
б) y = -корень х, х принадлежит (0; +бесконечность) и х = y2, у принадлежит (-бесконечность; 0);
в) у = lnх, х принадлежит (0; +бесконечность) и х = еу, у принадлежит R.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
