Упр.334 ГДЗ Колягин Ткачёва 11 класс (Алгебра)
Решение #1
![Изображение 334. Найти наибольшее и наименьшее значения функции:1) f(x) = 2sinx + sin2x на отрезке [0;3пи/2];2) f(x) = 2cosx + sin 2х на отрезке [0; пи];3) f(x) = 3sin х +...](/reshebniki/algebra/11/kolyagin/images1/334.png "Изображение ответа 334. Найти наибольшее и наименьшее значения функции:1) f(x) = 2sinx + sin2x на отрезке [0;3пи/2];2) f(x) = 2cosx + sin 2х на отрезке [0; пи];3) f(x) = 3sin х +...")
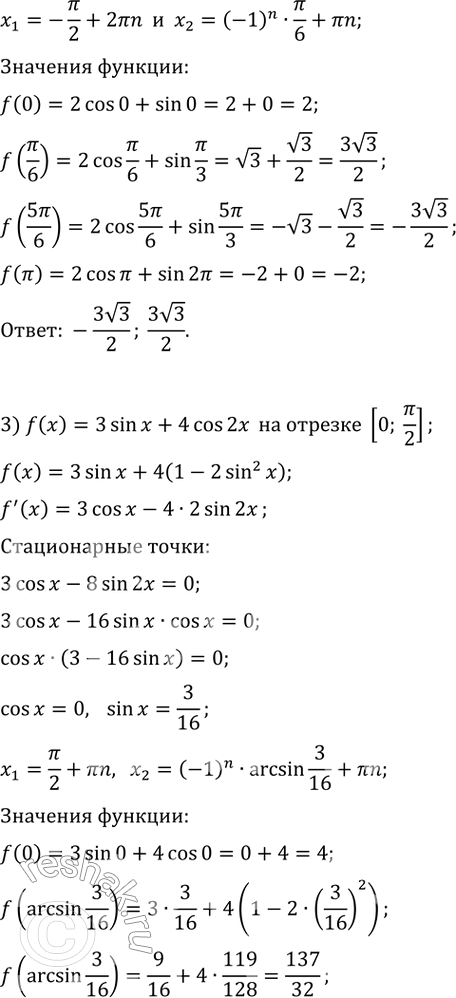
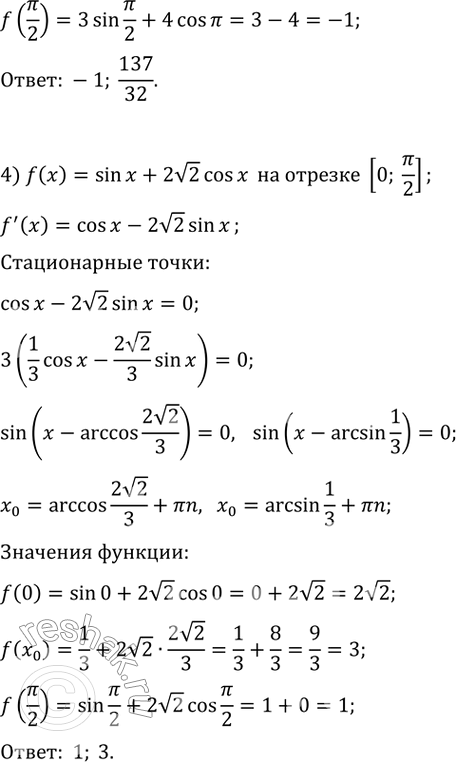
Решение #2
![Изображение 334. Найти наибольшее и наименьшее значения функции:1) f(x) = 2sinx + sin2x на отрезке [0;3пи/2];2) f(x) = 2cosx + sin 2х на отрезке [0; пи];3) f(x) = 3sin х +...](/reshebniki/algebra/11/kolyagin/images2/334.png "Изображение ответа 334. Найти наибольшее и наименьшее значения функции:1) f(x) = 2sinx + sin2x на отрезке [0;3пи/2];2) f(x) = 2cosx + sin 2х на отрезке [0; пи];3) f(x) = 3sin х +...")
Рассмотрим вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 11 класс, Просвещение:
334. Найти наибольшее и наименьшее значения функции:
1) f(x) = 2sinx + sin2x на отрезке [0;3пи/2];
2) f(x) = 2cosx + sin 2х на отрезке [0; пи];
3) f(x) = 3sin х + 4cos2x на отрезке [0; пи/2];
4) f(x) = sinx + 2 корень 2cosx на отрезке [0; пи/2].
Популярные решебники 11 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением