Задание 11 Параграф 20 ГДЗ Босова 10 класс (Информатика)
Решение #1
Рассмотрим вариант решения задания из учебника Босова 10 класс, Бином:
11. Сколько различных решений имеет система уравнений.
Введем новую переменную и применим для преобразования закон де Моргана:
y1=x1 & x2; (y1)=(x1) v(x2)
у2= x3 & x4
у3= x5 & x6
Второе уравнение системы выразим через импликацию. Уравнения системы принимают вид:
у1->у2=1
у2->у3=1
Соединяем в одно уравнение:
(у1->у2) & (у2->у3) =1
Для истинности этого уравнения не должна встречаться ситуация 1->0
Набор допустимых значений приведен в таблице.
Определяем, сколько есть решений, когда у=0, и сколько, когда у=1
Для 0 есть 3 решения (х1=0, х2=0; х1=0, х2=1; х1=1, х2=0)
Для 1 есть 1 решение (х1=1, х2=1)
Исходя из этого, определяем количество решений для каждого набора в таблице
Всего решений: 27+9+3+1=40
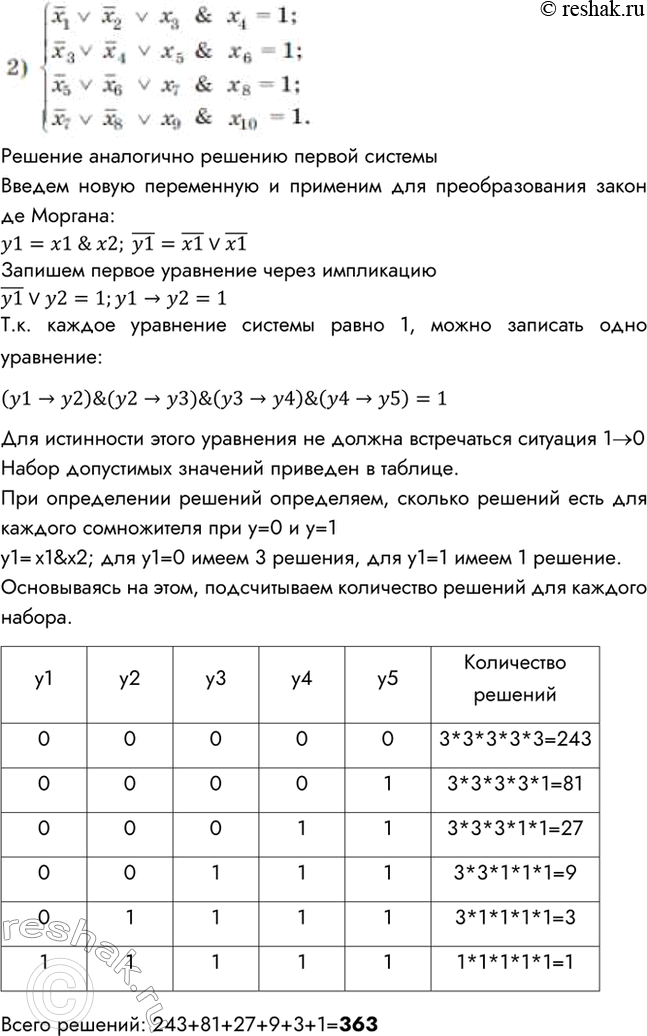
Решение аналогично решению первой системы
Введем новую переменную и применим для преобразования закон де Моргана:
y1=x1 & x2; (y1)=(x1) v(x1)
Запишем первое уравнение через импликацию
(y1) vy2=1;y1>y2=1
Т.к. каждое уравнение системы равно 1, можно записать одно уравнение:
(y1>y2)&(y2>y3)&(y3>y4)&(y4>y5)=1
Для истинности этого уравнения не должна встречаться ситуация 1->0
Набор допустимых значений приведен в таблице.
При определении решений определяем, сколько решений есть для каждого сомножителя при у=0 и у=1
у1= x1&x2; для у1=0 имеем 3 решения, для у1=1 имеем 1 решение.
Основываясь на этом, подсчитываем количество решений для каждого набора.
Всего решений: 243+81+27+9+3+1=363
Похожие решебники
Популярные решебники 10 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением