Упр.10.3 ГДЗ Никольский Потапов 11 класс (Алгебра)
Решение #1
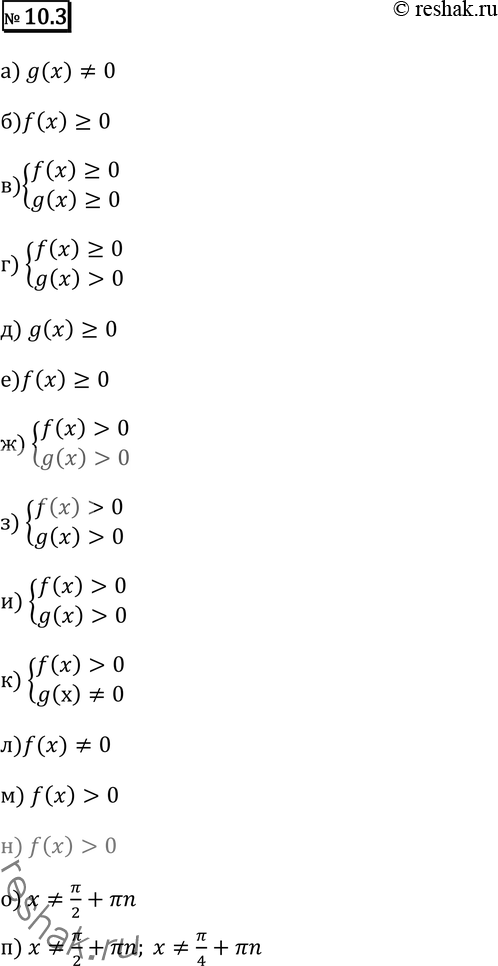
Рассмотрим вариант решения задания из учебника Никольский, Потапов 11 класс, Просвещение:
10.3 Какими условиями задается множество М, на котором равносильны (а > 0, а =/ 1) уравнения:
а) f(x)/g(x) = фи (х) и f(x) = g(x) фи (x);
б) корень f(x) = фи (х) и f(x) = фи^2 (х);
в) (корень f(x)) (корень g(x)) = фи(x) и корень (f(x)g(x))= фи(x);
г) (корень f(x))/ (корень g(x)) = фи(x) и корень (f(x)/g(x))= фи(x);
д) f(x) + (корень g(x)) = фи(x) + корень g(x) и f(x) = фи(x);
е) корень (f(x))2 = фи(x) и f(x) = фи(х);
ж) logaf(x) = logag(x) и f(x) = g(x);
з) logaf(x) + loga g (x) = фи(x) и loga (f(x)g(x)) = фи(х);
и) logaf(x) - loga g (x) = фи(x) и loga (f(x)/g(x)) = фи(х);
к) 1/logf(x)a = фи(x) и logaf(x)=фи(x);
л) loga (f(x))2 = фи(x) и 2 loga|f(x)| = фи (x);
м) 2 loga f(x) = фи(x) и loga (f(x))2 = фи (х);
н) aloga f(x) = фи(x) и f(x) = фи(х);
о) (1-tg2x)/(1+tg2x) = фи(x) и cos2x = фи(x);
п) 2tgx/(1-tg2x) = фи(x) и tg2x = фи(x)?
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
