Упр.3.12 ГДЗ Мордковича 10 класс профильный уровень (Алгебра)
Решение #1
Решение #2(записки учителя)
Решение #3(записки школьника)
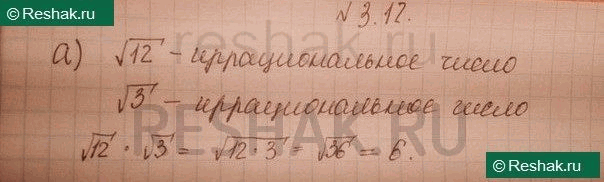
Рассмотрим вариант решения задания из учебника Мордкович, Семенов 10 класс, Мнемозина:
а) Докажите, что для любого иррационального числа а, найдется такое рациональное число P, что произведение ар — рациональное число.
б) Докажите, что если точка (x; у) лежит на прямой у = kx + b, где k =/0, b — рациональные числа, то числа x и у или оба рациональные, или оба иррациональные.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
