Упр.926 ГДЗ Макарычев Миндюк 8 класс (Алгебра)
Решение #1 (Учебник 2024)
Решение #2 (Учебник 2024)
Решение #3 (Учебник 2024)
Решение #4 (Учебник 2019)
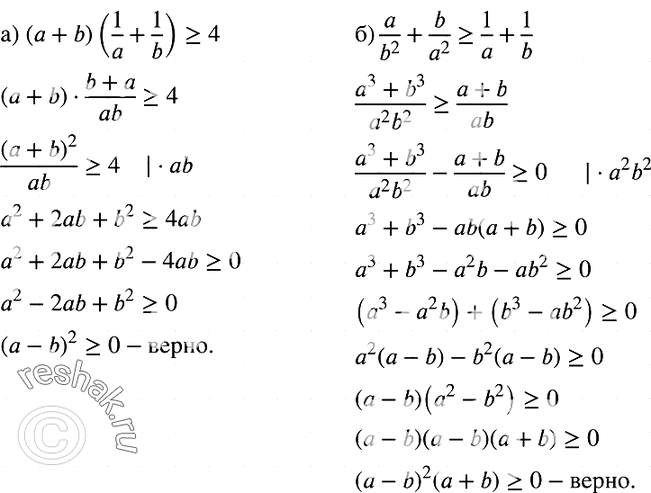
Решение #5 (Учебник 2019)
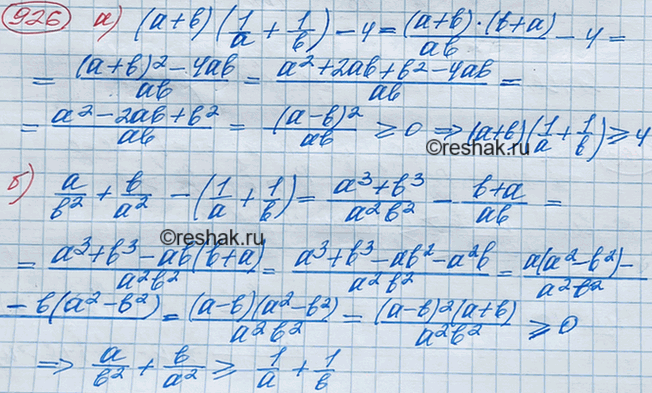
Рассмотрим вариант решения задания из учебника Макарычев, Миндюк, Нешков 8 класс, Просвещение:
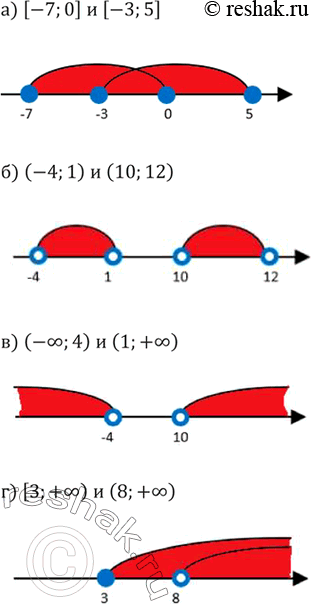
Покажите штриховкой на координатной прямой объединение промежутков:
а) [-7; 0] и [-3; 5];
б) (-4; 1) и (10; 12);
в) (-бесконечность; 4) и (10; +бесконечность);
г) [3; +бесконечность) и (8; +бесконечность).
Докажите, что при а > 0 и b > 0 верно неравенство:
а) (a+b)(1/a+1/b)>=4;
б) a/b2 + b/b2 >=1/a+1/b.
Похожие решебники
Популярные решебники 8 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением