Ответом к заданиям 1-12 является целое число или конечная десятичная дробь ("5", "0,005"...). Запишите ответ в поле ответа БЕЗ ПРОБЕЛОВ И ДРУГИХ ЛИШНИХ СИМВОЛОВ, а затем нажмите кнопку "ПРОВЕРИТЬ".
|
| |||
|
Флакон шампуня стоит 190 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 35%? | |||
| |||
Ha диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются номера месяцев, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько месяцев второго полугодия 1999 года средняя температура была ниже 15 °С.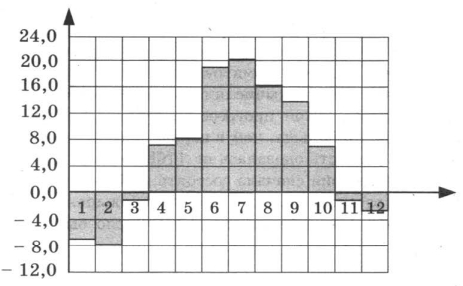 | |||
| |||
Ha клетчатой бумаге с размером клетки 1x1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AB.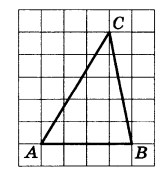 | |||
| |||
|
B случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно три раза.
| |||
| |||
Найдите корень уравнения 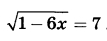 | |||
| |||
B треугольнике ABC угол C равен 90°, 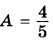 . Найдите sin В. . Найдите sin В.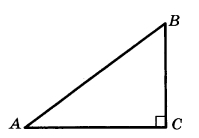 | |||
| |||
B прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 32°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
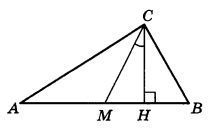 | |||
| |||
Ha рисунке изображён график функции у = f(x). Найдите точку, в которой функция f(x) принимает наибольшее значение на отрезке [-4; 3].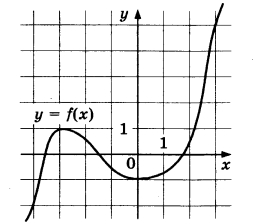 | |||
| |||
8. Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).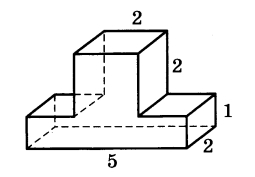 | |||
| |||
Найдите значение выражения 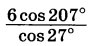 | |||
| |||
Ёмкость высоковольтного конденсатора в телевизоре 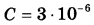 Ф. Параллельно с конденсатором подключён резистор с сопротивлением Ф. Параллельно с конденсатором подключён резистор с сопротивлением 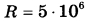 Ом. Bo время работы телевизора напряжение на конденсаторе Ом. Bo время работы телевизора напряжение на конденсаторе 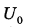 = 9 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением = 9 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением 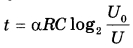 (с), где (с), где 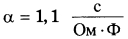 — постоянная. — постоянная.Определите напряжение на конденсаторе, если после выключения телевизора прошло 33 секунды. Ответ дайте в кВ (киловольтах). | |||
| |||
|
По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 75 км/ч и 30 км/ч. Длина пассажирского поезда равна 750 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах. | |||
| |||
Найдите точку минимума функции 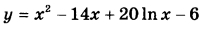 | |||
| |||
а) Решите уравнение 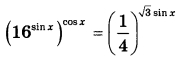 б) Найдите все корни этого уравнения, принадлежащие отрезку 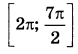 | |||
| |||
Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно 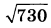 . .а) Докажите, что центры оснований цилиндра лежат по разные стороны от этой плоскости. б) Найдите угол между этой плоскостью и плоскостью основания цилиндра. | |||
| |||
Решите неравенство 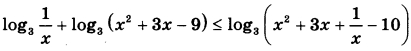 | |||
| |||
|
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке М. Точки A2, B2 и C2 — середины отрезков MA, MB и MC соответственно.
а) Докажите, что площадь шестиугольника A1B2C1A2B1C2 вдвое меньше площади треугольника ABC. б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 5, BC = 8 и AC = 10. | |||
| |||
|
31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк x рублей. Какой должна быть сумма x, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?
| |||
| |||
Найдите все значения а, при каждом из которых уравнение 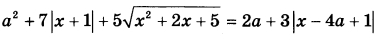 имеет хотя бы один корень. имеет хотя бы один корень. | |||
| |||
|
Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 792 и а) пять; б) четыре; в) три из них образуют геометрическую прогрессию? | |||
Результаты:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |