Ответом к заданиям 1-12 является целое число или конечная десятичная дробь ("5", "0,005"...). Запишите ответ в поле ответа БЕЗ ПРОБЕЛОВ И ДРУГИХ ЛИШНИХ СИМВОЛОВ, а затем нажмите кнопку "ПРОВЕРИТЬ".
|
| |||
|
B розницу один номер еженедельного журнала «Репортаж» стоит 26 руб., а полугодовая подписка на этот журнал стоит 590 руб. За полгода выходит 25 номеров журнала. Сколько рублей сэкономит Иванов за полгода, если не будет покупать каждый номер журнала отдельно, а оформит подписку? | |||
| |||
При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. Ha рисунке показана зависимость напряжения в цепи от времени работы фонарика. Ha горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, какое напряжение будет в цепи через 5 часов работы фонарика. Ответ дайте в вольтах.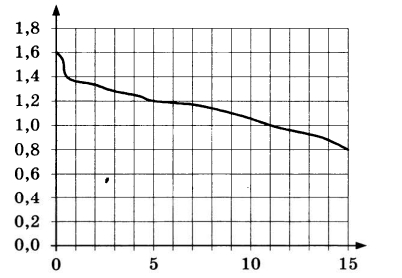 | |||
| |||
Найдите площадь трапеции с вершинами (1; 1), (2; 4), (10; 4), (3; 1).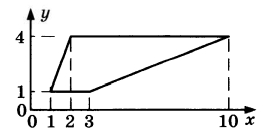 | |||
| |||
|
Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 4, но не дойдя до отметки 7. | |||
| |||
Найдите корень уравнения 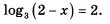 | |||
| |||
B четырёхугольник ABCD вписана окружность, AB = 6, BC = 4 и CD = 16. Найдите четвёртую сторону четырёхугольника.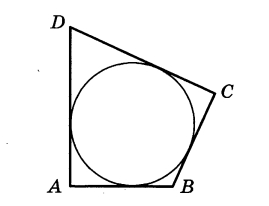 | |||
| |||
Ha рисунке изображён график функции у = f(x), определённой на интервале (-5; 9). Найдите количество точек, в которых производная функции f(x) равна 0.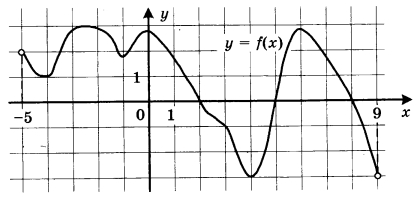 | |||
| |||
B правильной треугольной пирамиде SABC с основанием ABC точка P — середина ребра AB, S — вершина. Известно, что BC = 4, а площадь боковой поверхности равна 24. Найдите длину отрезка SP.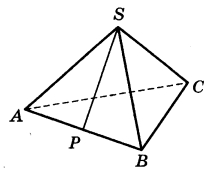 | |||
| |||
Найдите значение выражения 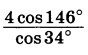 | |||
| |||
Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе показателей информативности In, оперативности Op, объективности Tr публикаций, а также качества Q сайта. Каждый отдельный показатель — целое число от -2 до 2. Составители рейтинга считают, что объективность ценится вдвое, а информативность публикаций — втрое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид 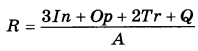
Найдите, каким должно быть число A, чтобы издание, у которого все показатели максимальны, получило бы рейтинг 1. | |||
| |||
|
Первая труба наполняет бак объёмом 600 литров, а вторая труба — бак объёмом 900 литров. Известно, что одна из труб пропускает в минуту на 3 л воды больше, чем другая. Сколько литров воды в минуту пропускает вторая труба, если баки были наполнены за одно и то же время? | |||
| |||
B какой точке 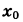 функция функция 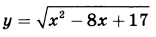 принимает наименьшее значение? принимает наименьшее значение? | |||
| |||
а) Решите уравнение 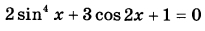 . .б) Найдите все корни этого уравнения, принадлежащие отрезку 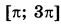 . . | |||
| |||
Площадь основания ABCD правильной четырёхугольной пирамиды SABCD равна 64, а площадь сечения пирамиды плоскостью SAC равна 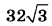 . .а) Докажите, что угол между плоскостью основания пирамиды и боковым ребром равен 60°. б) Найдите площадь боковой поверхности пирамиды. | |||
| |||
Решите неравенство 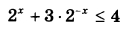 | |||
| |||
|
Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точке А, а вторую — в точке D. Прямая, проходящая через точку Q параллельно AD, второй раз пересекает первую окружность в точке В, а вторую — в точке С.
а) Докажите, что четырёхугольник ABCD — параллелограмм. б) Найдите отношение BP : PC, если радиус первой окружности вдвое больше радиуса второй. | |||
| |||
|
1 января 2015 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая — 1-го числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. Ha какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс. рублей? | |||
| |||
Найдите все значения а, при каждом из которых уравнение 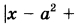 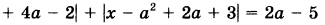 имеет хотя бы один корень на отрезке [5; 23]. имеет хотя бы один корень на отрезке [5; 23]. | |||
| |||
|
Имеется 8 карточек. На них записывают по одному каждое из чисел -1, 2, 4, -6, 7, -8, -10, 12. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел -1, 2, 4, -6, 7, -8, -10, 12. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.
а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться? | |||
Результаты:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |