Ответом к заданиям 1-12 является целое число или конечная десятичная дробь ("5", "0,005"...). Запишите ответ в поле ответа БЕЗ ПРОБЕЛОВ И ДРУГИХ ЛИШНИХ СИМВОЛОВ, а затем нажмите кнопку "ПРОВЕРИТЬ".
|
| |||
|
Для ремонта квартиры купили 42 рулона обоев. Какое наименьшее количество пачек обойного клея нужно купить, если одна пачка клея рассчитана на 8 рулонов? | |||
| |||
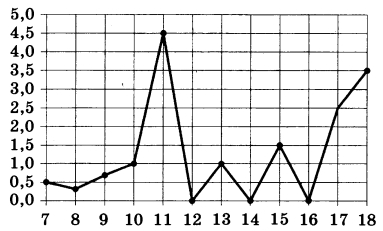
Ha рисунке жирными точками показано суточное количество осадков, выпадавших в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало больше 2 миллиметров осадков.
 | |||
| |||
Ha клетчатой бумаге с размером клетки 1x1 отмечены точки A, B и С. Найдите расстояние от точки A до прямой ВС.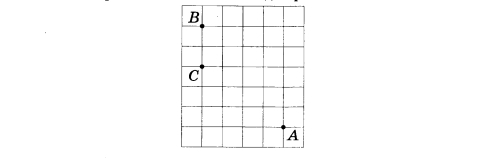 | |||
| |||
|
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 23 пассажиров, равна 0,85. Вероятность того, что окажется меньше 12 пассажиров, равна 0,62. Найдите вероятность того, что число пассажиров будет от 12 до 22. | |||
| |||
Найдите корень уравнения 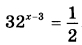 | |||
| |||
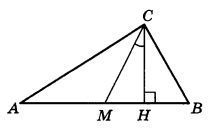
B прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 32°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
 | |||
| |||
Ha рисунке изображен график y = f\'(x) — производной функции
f(x), определенной на интервале (-4; 10). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у = -2x + 16 или совпадает с ней.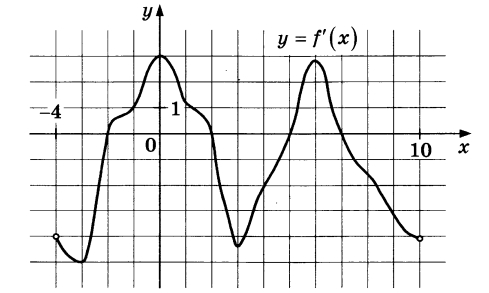 | |||
| |||
|
Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндра.
| |||
| |||
Найдите значение выражения 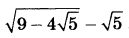 | |||
| |||
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 28 см. Расстояние 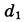 от линзы до лампочки может изменяться в пределах от 40 до 60 см, а расстояние от линзы до лампочки может изменяться в пределах от 40 до 60 см, а расстояние 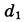 от линзы до экрана — в пределах от 53 до 77 см. Изображение на экране
будет чётким, если выполнено соотношение от линзы до экрана — в пределах от 53 до 77 см. Изображение на экране
будет чётким, если выполнено соотношение 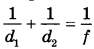 . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах. . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы её изображение на экране было чётким. Ответ выразите в сантиметрах. | |||
| |||
|
Игорь и Паша могут покрасить забор за 30 часов. Паша и Володя могут покрасить этот же забор за 36 часов, а Володя и Игорь — за 45 часов. За сколько часов мальчики покрасят забор, работая втроём? | |||
| |||
Найдите наибольшее значение функции 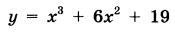 на отрезке на отрезке 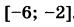 . . | |||
| |||
а) Решите уравнение 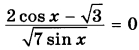 б) Найдите все корни этого уравнения, принадлежащие отрезку 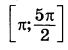 | |||
| |||
Дана правильная четырёхугольная пирамида MABCD с основанием ABCD, стороны основания которой равны 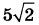 . Точка L — середина ребра MB. Тангенс угла между прямыми DM и AL равен . Точка L — середина ребра MB. Тангенс угла между прямыми DM и AL равен 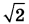 . .
а) Пусть O — центр основания пирамиды. Докажите, что прямые AO и LO перпендикулярны. б) Найдите высоту данной пирамиды. | |||
| |||
Решите неравенство 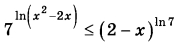 | |||
| |||
Медианы 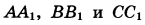 треугольника ABC пересекаются в точке М. Точки треугольника ABC пересекаются в точке М. Точки 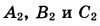 — середины отрезков MA, MB и MC соответственно. — середины отрезков MA, MB и MC соответственно.
а) Докажите, что площадь шестиугольника 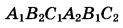 вдвое меньше площади треугольника ABC. вдвое меньше площади треугольника ABC.
б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 4, BC = 7 и AC = 8. | |||
| |||
|
15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно выплатить банку за первые 12 месяцев? | |||
| |||
Найдите все значения а, при каждом из которых наибольшее значение функции 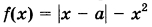 не меньше 1. не меньше 1. | |||
| |||
|
Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов. Затем математик добавил к этой прогрессии следующий её член и снова вычислил такую же разность.
а) Приведите пример такой прогрессии, если во второй раз разность оказалась на 48 больше, чем в первый раз. б) Bo второй раз разность оказалась на 1440 больше, чем в первый раз. Могла ли прогрессия сначала состоять из 12 членов? в) Bo второй раз разность оказалась на 1440 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала? | |||
Результаты:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |