Ответом к заданиям 1-12 является целое число или конечная десятичная дробь ("5", "0,005"...). Запишите ответ в поле ответа БЕЗ ПРОБЕЛОВ И ДРУГИХ ЛИШНИХ СИМВОЛОВ, а затем нажмите кнопку "ПРОВЕРИТЬ".
|
| |||
|
Флакон шампуня стоит 170 рублей. Какое наибольшее число флаконов можно купить на 900 рублей во время распродажи, когда скидка составляет 35%? | |||
| |||
Ha диаграмме показана средняя температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются номера месяцев, по вертикали — средняя температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с отрицательной средней температурой в 1994 году в Нижнем Новгороде. | |||
| |||
Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см x 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.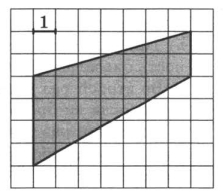 | |||
| |||
|
B случайном эксперименте бросают две игральные кости (кубика). Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых. | |||
| |||
Найдите корень уравнения 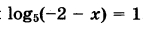 | |||
| |||
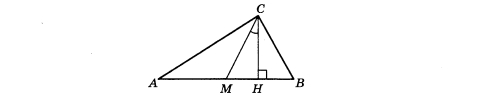
B прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 28°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.
 | |||
| |||
Ha рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке Xo.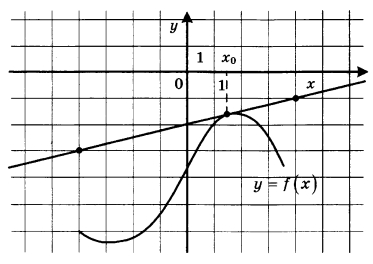 | |||
| |||
Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом 30°. Боковое ребро равно 3. Найдите диагональ призмы.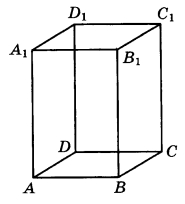 | |||
| |||
Найдите значение выражения 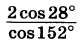 | |||
| |||
Для определения эффективной температуры звёзд используют закон Стефана—Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвёртой степени температуры: 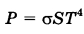 , где , где 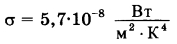 - постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь - постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь 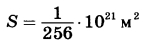 , а излучаемая ею мощность P равна , а излучаемая ею мощность P равна 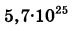 Вт. Определите температуру этой звезды. Ответ выразите в градусах Кельвина. Вт. Определите температуру этой звезды. Ответ выразите в градусах Кельвина. | |||
| |||
|
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 44 км/ч, а вторую половину пути — со скоростью, на 21 км/ч большей скорости первого, в результате чего прибыл в B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. | |||
| |||
Найдите наименьшее значение функции 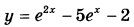 на отрезке на отрезке 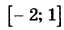 | |||
| |||
а) Решите уравнение 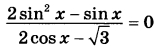 б) Найдите все корни этого уравнения, принадлежащие отрезку 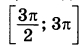 | |||
| |||
|
Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD с основанием ABCD равна 108, а площадь полной поверхности этой пирамиды равна 144.
а) Докажите, что угол между плоскостью SAC и плоскостью, проходящей через вершину S этой пирамиды, середину стороны AB и центр основания, равен 45°. б) Найдите площадь сечения пирамиды плоскостью SAC. | |||
| |||
Решите неравенство 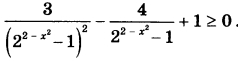 | |||
| |||
|
Ha катетах AC и BC прямоугольного треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина гипотенузы AB, H — точка пересечения прямых CM и DK. а) Докажите, что CM 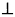 DK. DK.б) Найдите MH, если известно, что катеты треугольника ABC равны 30 и 40. | |||
| |||
|
15-го января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования? | |||
| |||
Найдите все значения а, при каждом из которых уравнение 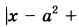 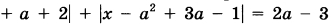 имеет корни, но ни один из них не принадлежит интервалу (4; 19). имеет корни, но ни один из них не принадлежит интервалу (4; 19). | |||
| |||
|
Возрастающая конечная арифметическая прогрессия состоит из различных целых неотрицательных чисел. Математик вычислил разность между квадратом суммы всех членов прогрессии и суммой их квадратов. Затем математик добавил к этой прогрессии следующий её член и снова вычислил такую же разность. а) Приведите пример такой прогрессии, если во второй раз разность оказалась на 40 больше, чем в первый раз. б) Bo второй раз разность оказалась на 1768 больше, чем в первый раз. Могла ли прогрессия сначала состоять из 13 членов? в) Bo второй раз разность оказалась на 1768 больше, чем в первый раз. Какое наибольшее количество членов могло быть в прогрессии сначала? | |||
Результаты:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |