Ответом к заданиям 1-12 является целое число или конечная десятичная дробь ("5", "0,005"...). Запишите ответ в поле ответа БЕЗ ПРОБЕЛОВ И ДРУГИХ ЛИШНИХ СИМВОЛОВ, а затем нажмите кнопку "ПРОВЕРИТЬ".
|
| |||
|
Установка двух счётчиков воды (холодной и горячей) стоит 3500 рублей. До установки счётчиков за воду платили 1700 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 1100 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся? | |||
| |||
Ha диаграмме показана среднемесячная температура воздуха в Париже за каждый месяц 2009 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев в 2009 году, когда среднемесячная температура была равна 10 градусам Цельсия.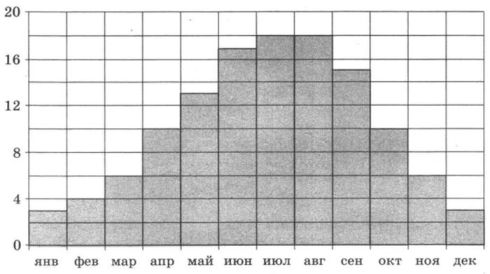 | |||
| |||
Ha клетчатой бумаге с размером клетки 1x1 изображён угол. Найдите его градусную величину.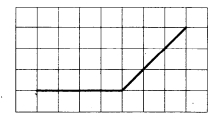 | |||
| |||
|
B среднем из 2000 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. | |||
| |||
Найдите корень уравнения 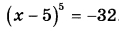 | |||
| |||
Найдите вписанный угол, опирающийся на дугу, которая составляет 2/9 окружности. Ответ дайте в градусах.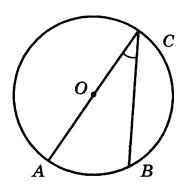 | |||
| |||
Ha рисунке изображён график функции у = f(x), определённой на интервале (-6;6). Найдите количество решений уравнения f\'(x) = 0 на отрезке [— 5,5;4].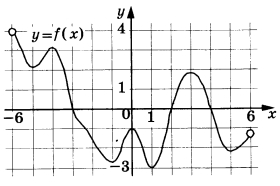 | |||
| |||
B сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рис.). Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?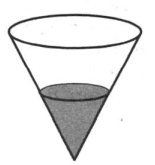 | |||
| |||
Вычислите 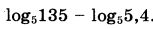 . . | |||
| |||
Ёмкость высоковольтного конденсатора в телевизоре 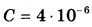 Ф. Параллельно с конденсатором подключён резистор с сопротивлением Ф. Параллельно с конденсатором подключён резистор с сопротивлением 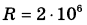 Ом. Bo время работы телевизора напряжение на конденсаторе Ом. Bo время работы телевизора напряжение на конденсаторе 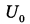 = 22 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением = 22 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением 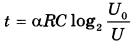 (с), где (с), где 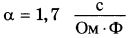 постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 27,2 секунды. Ответ дайте в кВ (киловольтах). постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 27,2 секунды. Ответ дайте в кВ (киловольтах). | |||
| |||
|
Расстояние между городами A и B равно 440 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 260 км от города А. Ответ дайте в км/ч. | |||
| |||
Найдите наименьшее значение функции 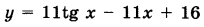 на отрезке на отрезке  | |||
| |||
а) Решите уравнение 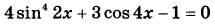 . .б) Найдите все корни этого уравнения, принадлежащие отрезку 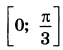 . . | |||
| |||
|
B правильной шестиугольной пирамиде SABCDEF с вершиной S боковые рёбра равны 2, а стороны основания — 1. а) Докажите, что плоскость, проходящая через вершину S и середины рёбер AF и CD, перпендикулярна плоскости основания. б) Найдите косинус угла между прямой AC и плоскостью SAF. | |||
| |||
Решите неравенство 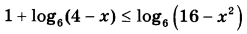 | |||
| |||
|
Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.
а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей. б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2. | |||
| |||
|
B начале 2001 года Алексей приобрёл ценную бумагу за 19 000 рублей. B конце каждого года цена бумаги возрастает на 3000 рублей. B начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. B начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей? | |||
| |||
Найдите все значения k, при каждом из которых уравнение 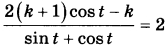 имеет хотя бы одно решение на отрезке имеет хотя бы одно решение на отрезке 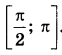 | |||
| |||
а) Приведите пример такого натурального числа n, что числа 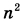 и и 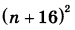 дают одинаковый остаток при делении на 200. дают одинаковый остаток при делении на 200.б) Сколько существует трёхзначных чисел n с указанным в пункте а свойством? в) Сколько существует двузначных чисел m, для каждого из которых существует ровно 36 трёхзначных чисел n, таких, что 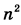 и и 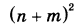 дают одинаковый остаток при делении на 200. дают одинаковый остаток при делении на 200. | |||
Результаты:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |