Ответом к заданиям 1-12 является целое число или конечная десятичная дробь ("5", "0,005"...). Запишите ответ в поле ответа БЕЗ ПРОБЕЛОВ И ДРУГИХ ЛИШНИХ СИМВОЛОВ, а затем нажмите кнопку "ПРОВЕРИТЬ".
|
| |||
|
Для покраски потолка требуется 270 г краски на 1 м2. Краска продаётся в банках по 3 кг. Сколько банок краски нужно купить для покраски потолка площадью 37 м2? | |||
| |||
На диаграмме показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по приведённой диаграмме разность между наибольшей и наименьшей среднемесячными температурами. Ответ дайте в градусах Цельсия.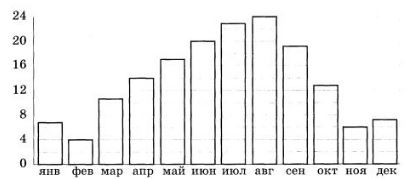 | |||
| |||
На клетчатой бумаге с размером клетки 1x1 изображён ромб. Найдите его площадь.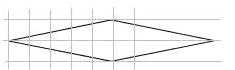 | |||
| |||
|
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. | |||
| |||
Найдите корень уравнения 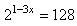 . . | |||
| |||
Угол АСО равен 27град, где О — центр окружности. Его сторона СА касается окружности. Сторона СО пересекает окружность в точке В (см. рис.). Найдите величину меньшей дуги АВ окружности. Ответ дайте в градусах.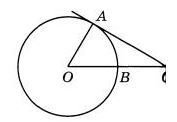 | |||
| |||
На рисунке изображён график функции y=f(x), определённой на интервале (-6; 6). Найдите количество решений уравнения f\'(х) = 0 на отрезке [-3,5; 4,5].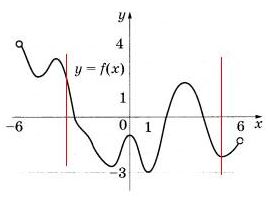 | |||
| |||
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 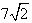 . Найдите радиус сферы. . Найдите радиус сферы.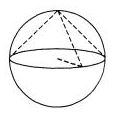 | |||
| |||
Найдите значение выражения 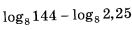 | |||
| |||
Водолазный колокол, содержащий в начальный момент времени v = 2 моля воздуха объёмом 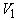 =10л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма =10л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма 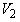 . Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле . Работа, совершаемая водой при сжатии воздуха, вычисляется по формуле 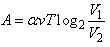 , где , где 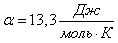 — постоянная, а Т = 300 К — температура воздуха. Найдите, какой объём — постоянная, а Т = 300 К — температура воздуха. Найдите, какой объём 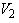 (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 15 960 Дж. (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 15 960 Дж. | |||
| |||
|
Расстояние между городами А и В равно 300 км. Из города А в город В выехал автомобиль, а через 1 час следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С. Ответ дайте в километрах. | |||
| |||
Найдите наибольшее значение функции 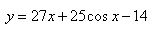 на отрезке на отрезке 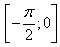 . . | |||
| |||
а) Решите уравнение 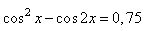 . .
б) Укажите корни этого уравнения, принадлежащие отрезку 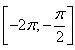 . . | |||
| |||
В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а боковое ребро SA равно 13. Точки М и N — середины рёбер SA и SB соответственно. Плоскость 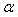 содержит прямую MN и перпендикулярна плоскости основания пирамиды. содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость а делит медиану CE основания в отношении 5:1, считая от точки С. б) Найдите площадь многоугольника, являющегося сечением пирамиды SABC плоскостью a. | |||
| |||
Решите неравенство 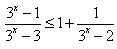 . . | |||
| |||
|
Четырехугольник ABCD вписан в окружность, причем сторона CD - диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность - в точке F, причем H - середина AE.
а) Докажите, что четырехугольник BCFE - параллелограмм. б) Найдите площадь четырехугольника ABCD, если известно, что AB = 5 и AH = 4. | |||
| |||
|
31 декабря 2014 года Алексей взял в банке 9 282 000 рублей в кредит под 10% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк X рублей. Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)? | |||
| |||
Найдите все значения а, при каждом из которых система уравнений 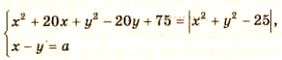 имеет более одного решения. имеет более одного решения. | |||
| |||
|
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел? б) Могут ли быть одинаковыми все три значения средних арифметических? в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических. | |||
Результаты:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |