Ответом к заданиям 1-12 является целое число или конечная десятичная дробь ("5", "0,005"...). Запишите ответ в поле ответа БЕЗ ПРОБЕЛОВ И ДРУГИХ ЛИШНИХ СИМВОЛОВ, а затем нажмите кнопку "ПРОВЕРИТЬ".
|
| |||
|
Для приготовления абрикосового варенья на 1 кг абрикосов нужно 1,2 кг сахара. Какое наименьшее количество килограммовых упаковок сахара нужно, чтобы сварить варенье из 14 кг абрикосов? | |||
| |||
На рисунке жирными точками показано суточное количество осадков, выпадающих в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней за данный период не выпадало осадков.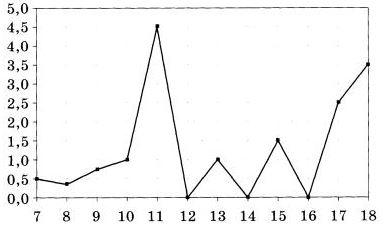 | |||
| |||
На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.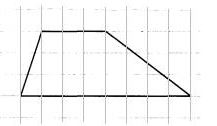 | |||
| |||
|
Из множества натуральных чисел от 28 до 47 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3? | |||
| |||
Найдите корень уравнения 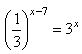 | |||
| |||
В треугольнике ABC АВ = ВС, АС = 16, высота СН равна 4. Найдите синус угла АСВ.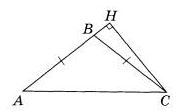 | |||
| |||
На рисунке изображён график у=f\'(x) — производной функции f(x), определённой на интервале (-11;6). Найдите количество точек минимума функции f(x) принадлежащих отрезку [-6;4].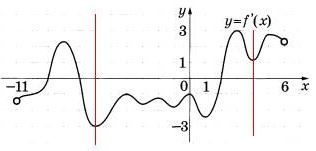 | |||
| |||
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 79. Найдите площадь боковой поверхности исходной призмы.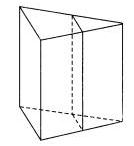 | |||
| |||
Найдите значение выражения 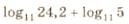 | |||
| |||
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 299 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле 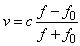 , где с = 1500 м/с — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите наибольшую возможную частоту отражённого сигнала f, если скорость погружения батискафа не должна превышать 5 м/с. Ответ выразите в МГц. , где с = 1500 м/с — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите наибольшую возможную частоту отражённого сигнала f, если скорость погружения батискафа не должна превышать 5 м/с. Ответ выразите в МГц. | |||
| |||
|
От пристани А к пристани В, расстояние между которыми равно 153 км, отправился с постоянной скоростью первый теплоход, а через 8 часов после этого следом за ним со скоростью на 8 км/ч большей отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч. | |||
| |||
Найдите наибольшее значение функции 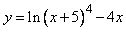 на отрезке [-4,5; 0] . на отрезке [-4,5; 0] . | |||
| |||
а) Решите уравнение 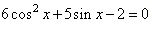 . .
б) Укажите корни этого уравнения, принадлежащие отрезку 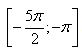 . . | |||
| |||
|
В правильной четырехугольной призме ABCA1B1C1D1 стороны основания равны 2, а боковые ребра равны 3. На ребре AA1 отмечена точка E так, что AE:EA1=1:2.
а) Постройте прямую пересечения плоскостей ABC и BED1. б) Найдите угол между плоскостями ABC и BED1. | |||
| |||
Решите неравенство 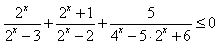 . . | |||
| |||
Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC=CD.
а) Докажите, что AB:BC=AP:PD.
б) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB=5,
а BC=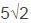 | |||
| |||
|
В начале 2001 года Алексей приобрёл ценную бумагу за 11 000 рублей. В конце каждого года цена бумаги возрастает на 4000 рублей. В начале любого года Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. В начале какого года Алексей должен продать ценную бумагу, чтобы через пятнадцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей? | |||
| |||
Найдите все значения a, при каждом из которых уравнение 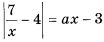 на промежутке на промежутке 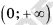 имеет более двух корней. имеет более двух корней. | |||
| |||
|
На доске было написано 30 натуральных чисел (необязательно различных), каждое из которых не превосходит 40. Среднее арифметическое написанных чисел равнялось 7. Вместо каждого из чисел на доске написано число, в два раза меньшее первоначального. Числа, которые после этого оказались меньше 1, с доски стерли. а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше 14? б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше 12, но меньше 13? в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске. | |||
Результаты:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |