Урок 1 Часть 3 ГДЗ Петерсон 4 класс (2015) (Математика)

|
Не совпадает с вашим учебником? Посмотрите обновленный. |
Решение #1






Рассмотрим вариант решения задания из учебника Петерсон 4 класс, Просвещение:
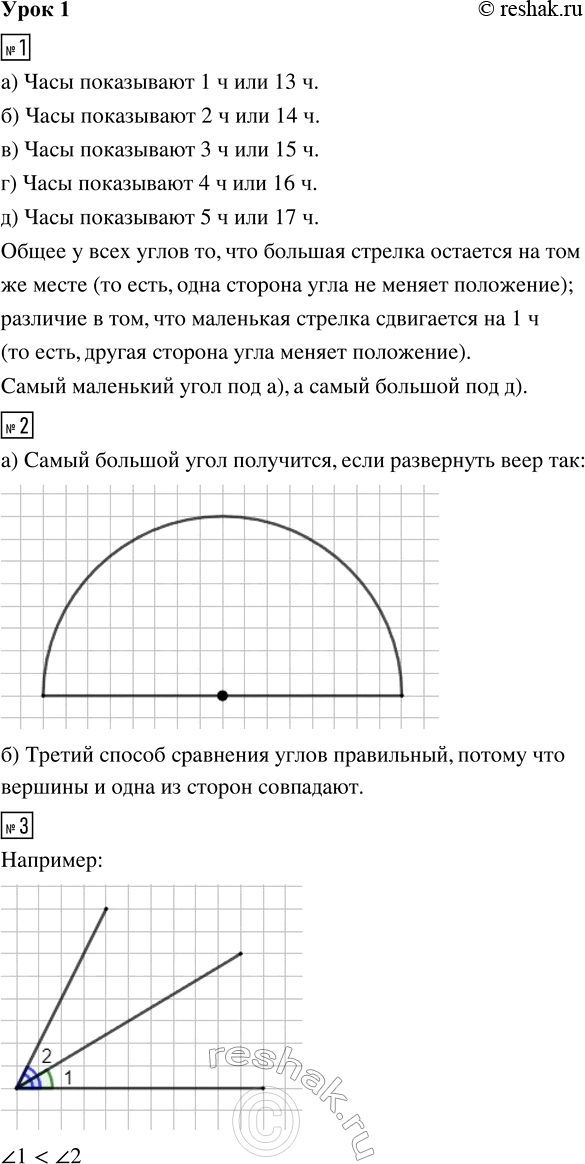
1. Определи по рисункам время, которое показывают часы. Обозначь дугой на каждом рисунке выделенный цветом угол, образованный стрелками часов.
Что общего и что различного у всех этих углов? Какой из них самый маленький, а какой — самый большой?
2. а) Сложи из бумаги веер. Разверни его так, чтобы получился самый большой из возможных углов.
б) Таня и Оля стали спорить, чей веер образует больший угол. Они наложили один веер на другой разными способами.
Как ты думаешь, какой из этих способов сравнения углов правильный? Почему?
3. Вырежь из бумаги два произвольных угла. Определи с помощью наложения, какой из них больше, а какой меньше.
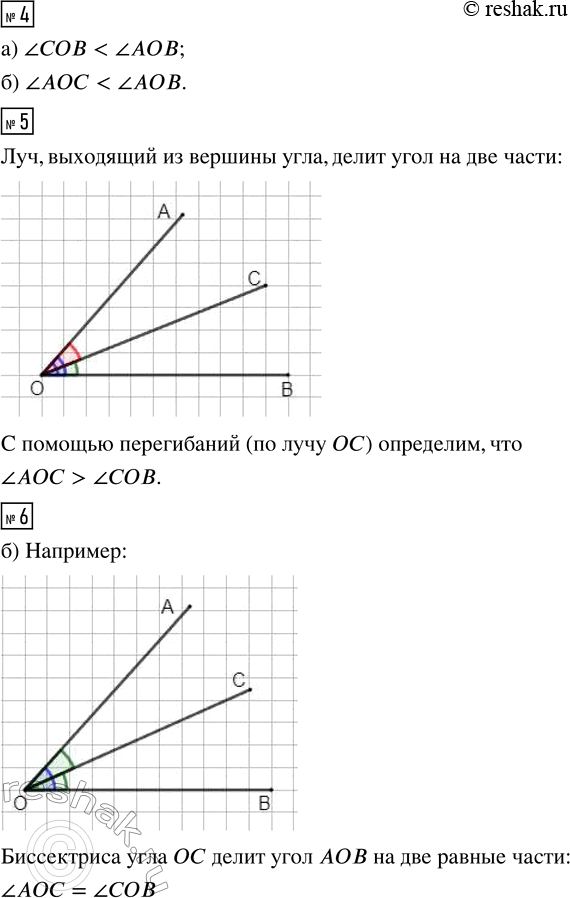
4. Сравни углы:
?COB и ?AOB; ?AOC и ?AOB.
5. Вырежь из бумаги угол. Проведи луч, выходящий из его вершины. На сколько частей этот луч делит угол? Сравни получившиеся углы перегибанием листа.
6. а) Вырежь из бумаги угол и перегни его так, чтобы стороны угла совпали. Полученный луч делит угол на 2 равные части. Этот луч называется биссектрисой.
б) Начерти на листе бумаги угол. Построй на глаз его биссектрису. Проверь правильность построения перегибанием листа.
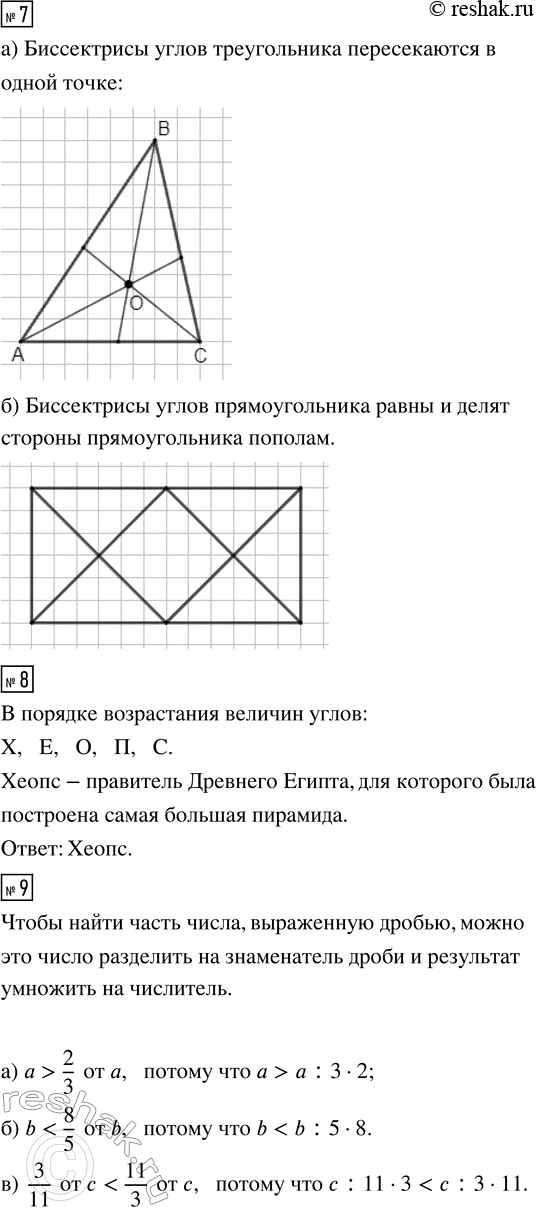
7. а) Вырежь из листа бумаги треугольник. Построй перегибанием листа биссектрисы его углов.
б) Вырежь из листа бумаги прямоугольник. Построй перегибанием листа биссектрисы его углов.
Какие закономерности ты наблюдаешь?
8. Сравни на глаз углы. Расположи соответствующие буквы в порядке возрастания величин углов, и ты узнаешь имя знаменитого правителя Древнего Египта, для которого была построена самая большая пирамида.
9. а) Что больше — число а или 2/3 от а? Почему?
б) Что больше — число b или 8/5 от b? Почему?
в) Что больше — 3/11 от с или 11/3 от c? Почему?
10. Как найти часть от числа, выраженную дробью? Вычисли:
7/8 от 240 [О] 9/7 от 56 [Р] 14 % от 4000 [Ж]
5/6 от 90 [Е] 17/12 от 84 [С] 134 % от 800 [Д]
Расположив ответы примеров в порядке убывания и сопоставив им соответствующие буквы, ты узнаешь имя египетского фараона, в честь которого была построена самая первая пирамида.
11. Александр Великий, царь Македонии, был широко известен своими завоевательными походами. Однажды среди трофеев у него оказалось 2000 золотых монет: больших, средних и маленьких. Большие монеты составили 35 % от общего числа монет, а средние монеты — 17/20 от числа больших монет. Сколько было маленьких монет? Каких монет у Александра Македонского оказалось больше — маленьких или больших, и на сколько?
12. а) Верблюд может отложить в горбу жир, который он использует затем при недостатке корма. Масса этого жира достигает 20 % массы верблюда. Какое максимальное количество жира может отложить в горбу верблюд, если его масса равна 600 кг?
б) Масса верблюда 700 кг, а масса груза, который он несет на спине, составляет 40 % массы верблюда. Чему равна масса верблюда вместе с грузом?
13. Найди закономерность и заполни таблицу. Запиши формулу зависимости между переменными х и у:
14. Выполни действия:
а) 82 а 6 м^2 + 47 а 98 м^2 + 3 га;
б) 2 т 5 ц 4 кг - 18 ц 37 кг;
в) 3 м 6 см 9 мм · 9;
г) 10 ч 44 мин 48 с : 48.
15. А — множество натуральных решений неравенства 3 < x ? 7, В — множество натуральных решений неравенства 5 ? x ? 9. Запиши множества А и В с помощью фигурных скобок, найди их объединение и пересечение.
16. Является ли число 103 решением неравенства:
(1500 · 50 - 18 388 + 637 · 504)/((38 685 + 199 405) : 58) ? x < (7 179 630 : 89 - (490 000 : 7 + 3558))/(54 648 : 792)?
Сколько натуральных решений имеет это неравенство? Приведи пример какого-нибудь решения, которое не является натуральным числом.
17. Мышке до норки 20 шагов. Кошке до мышки 5 прыжков. За один прыжок кошки мышка делает 3 шага. Один прыжок кошки равен 10 шагам мышки. Догонит ли кошка мышку?
Похожие решебники
Популярные решебники 4 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







