—тр.98 „асть 2 √ƒ« ƒорофеев ћиракова 4 класс (ћатематика)
–ешение #1


–ешение #2





–ассмотрим вариант решени€ задани€ из учебника ƒорофеев, ћиракова, Ѕука 4 класс, ѕросвещение:
5. –Я–µ—А–≤—Л–є –Љ–∞–ї—М—З–Є–Ї –љ–∞ –Ї–Њ–љ—М–Ї–∞—Е –њ—А–Њ–±–µ–≥–∞–µ—В 8 –Љ –≤ —Б–µ–Ї—Г–љ–і—Г, –∞ –≤—В–Њ—А–Њ–є вАФ 6 –Љ –≤ —Б–µ–Ї—Г–љ–і—Г. –І–µ—А–µ–Ј —Б–Ї–Њ–ї—М–Ї–Њ —Б–µ–Ї—Г–љ–і –њ–µ—А–≤—Л–є –Љ–∞–ї—М—З–Є–Ї –Њ–њ–µ—А–µ–і–Є—В –≤—В–Њ—А–Њ–≥–Њ –љ–∞ 50 –Љ, –µ—Б–ї–Є –Њ–љ–Є –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –њ–Њ–±–µ–≥—Г—В —Б –Њ–і–љ–Њ–≥–Њ –Љ–µ—Б—В–∞ –Є –≤ –Њ–і–љ–Њ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є?
–°–Њ—Б—В–∞–≤—М –Є —А–µ—И–Є –Ј–∞–і–∞—З—Г, –Њ–±—А–∞—В–љ—Г—О –і–∞–љ–љ–Њ–є.
6. –°—А–∞–≤–љ–Є.
57 —Ж 7 –Ї–≥ –Є 57 070 –Ї–≥ 57 –Љ–Є–љ 7 —Б –Є 5 770 –Љ–Є–љ
57 —В 7 –Ї–≥ –Є 57 007 –Ї–≥ 57 –Љ 7 –Љ–Љ –Є 5 707 –Љ–Љ
7. –Э–∞ –њ–µ—А–≤–Њ–Љ —В—А–∞–Ї—В–Њ—А–µ —А–∞–±–Њ—В–∞–ї–Є 60 —З, –љ–∞ –≤—В–Њ—А–Њ–Љ вАФ 55 —З. –Э–∞ –≤—В–Њ—А–Њ–Љ —В—А–∞–Ї—В–Њ—А–µ –Є–Ј—А–∞—Б—Е–Њ–і–Њ–≤–∞–ї–Є –љ–∞ 40 –ї –≥–Њ—А—О—З–µ–≥–Њ –Љ–µ–љ—М—И–µ, —З–µ–Љ –љ–∞ –њ–µ—А–≤–Њ–Љ. –°–Ї–Њ–ї—М–Ї–Њ –ї–Є—В—А–Њ–≤ –≥–Њ—А—О—З–µ–≥–Њ –Є–Ј—А–∞—Б—Е–Њ–і–Њ–≤–∞–ї–Є –љ–∞ –Ї–∞–ґ–і–Њ–Љ —В—А–∞–Ї—В–Њ—А–µ –њ—А–Є –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ–є –љ–Њ—А–Љ–µ —А–∞—Б—Е–Њ–і–∞ –≥–Њ—А—О—З–µ–≥–Њ –≤ —З–∞—Б?
8. –Т—Л—Б–Њ—В–∞ —Д—Г—В–±–Њ–ї—М–љ—Л—Е –≤–Њ—А–Њ—В 2 –Љ 44 —Б–Љ, –∞ –≤—Л—Б–Њ—В–∞ —Е–Њ–Ї–Ї–µ–є–љ—Л—Е –≤–Њ—А–Њ—В –≤ 2 —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ. –Т—Л—З–Є—Б–ї–Є –≤—Л—Б–Њ—В—Г —Е–Њ–Ї–Ї–µ–є–љ—Л—Е –≤–Њ—А–Њ—В.
9. –Ъ–∞–Ї –љ—Г–ґ–љ–Њ —А–∞—Б—Б—В–∞–≤–Є—В—М —Б–Ї–Њ–±–Ї–Є, —З—В–Њ–±—Л –Ј–∞–њ–Є—Б—М —Б—В–∞–ї–∞ –≤–µ—А–љ–Њ–є?
350 - 15 ¬Ј 104 - 1 428 : 14 = 320
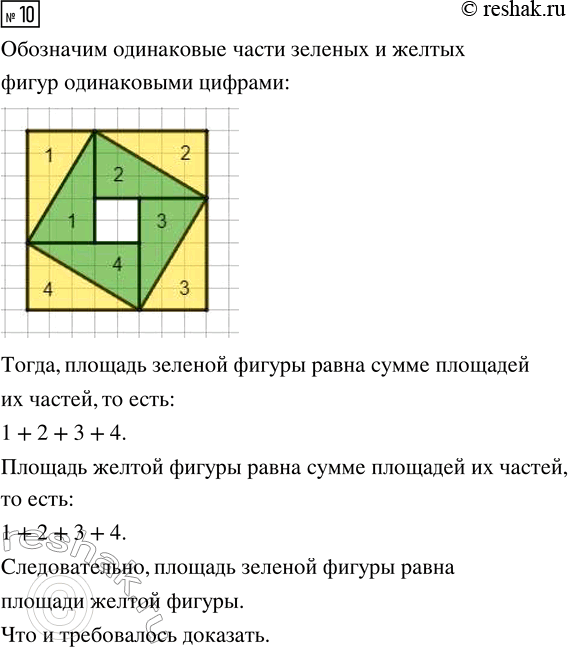
10. –Ф–Њ–Ї–∞–ґ–Є, —З—В–Њ –њ–ї–Њ—Й–∞–і—М –Ј–µ–ї—С–љ–Њ–є —Д–Є–≥—Г—А—Л —А–∞–≤–љ–∞ –њ–ї–Њ—Й–∞–і–Є –ґ—С–ї—В–Њ–є —Д–Є–≥—Г—А—Л.
5.
–Ч–∞–њ–Є—И–µ–Љ –Ї—А–∞—В–Ї–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –Ј–∞–і–∞—З–Є.
–Ь–∞–ї—М—З–Є–Ї–Є –±–µ–≥—Г—В –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –≤ –Њ–і–љ–Њ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є
–°–Ї–Њ—А–Њ—Б—В—М –њ–µ—А–≤–Њ–≥–Њ - 8 –Љ/—Б
–°–Ї–Њ—А–Њ—Б—В—М –≤—В–Њ—А–Њ–≥–Њ - 6 –Љ/—Б
–†–∞—Б—Б—В–Њ—П–љ–Є–µ, –љ–∞ –Ї–Њ—В–Њ—А–Њ–µ –њ–µ—А–≤—Л–є –Њ–њ–µ—А–µ–і–Є–ї –≤—В–Њ—А–Њ–≥–Њ - 50 –Љ
–Т—А–µ–Љ—П, —З–µ—А–µ–Ј –Ї–Њ—В–Њ—А–Њ–µ –њ–µ—А–≤—Л–є –Њ–њ–µ—А–µ–і–Є–ї –≤—В–Њ—А–Њ–≥–Њ - ?
–Я—А–Є –і–≤–Є–ґ–µ–љ–Є–Є —Б –Њ—В—Б—В–∞–≤–∞–љ–Є–µ–Љ —Б–Ї–Њ—А–Њ—Б—В—М —Г–і–∞–ї–µ–љ–Є—П —А–∞–≤–љ–∞ —А–∞–Ј–љ–Њ—Б—В–Є —Б–Ї–Њ—А–Њ—Б—В–µ–є.
–Э–∞–є–і—С–Љ —Б–Ї–Њ—А–Њ—Б—В—М —Г–і–∞–ї–µ–љ–Є—П. –Ф–ї—П —Н—В–Њ–≥–Њ –≤—Л—З—В–µ–Љ –Є–Ј —Б–Ї–Њ—А–Њ—Б—В–Є –њ–µ—А–≤–Њ–≥–Њ –Љ–∞–ї—М—З–Є–Ї–∞ —Б–Ї–Њ—А–Њ—Б—В—М –≤—В–Њ—А–Њ–≥–Њ.
8-6=2 (–Љ/—Б) вАУ —Б–Ї–Њ—А–Њ—Б—В—М —Г–і–∞–ї–µ–љ–Є—П.
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –љ–∞–є—В–Є –≤—А–µ–Љ—П –њ–Њ –Є–Ј–≤–µ—Б—В–љ—Л–Љ —А–∞—Б—Б—В–Њ—П–љ–Є—О –Є —Б–Ї–Њ—А–Њ—Б—В–Є, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —А–∞—Б—Б—В–Њ—П–љ–Є–µ —А–∞–Ј–і–µ–ї–Є—В—М –љ–∞ —Б–Ї–Њ—А–Њ—Б—В—М.
–†–∞–Ј–і–µ–ї–Є–Љ —А–∞—Б—Б—В–Њ—П–љ–Є–µ, –љ–∞ –Ї–Њ—В–Њ—А–Њ–µ –њ–µ—А–≤—Л–є –Њ–њ–µ—А–µ–і–Є–ї –≤—В–Њ—А–Њ–≥–Њ, –љ–∞ —Б–Ї–Њ—А–Њ—Б—В—М —Г–і–∞–ї–µ–љ–Є—П.
50вИґ2=25 (—Б) вАУ –≤—А–µ–Љ—П, —З–µ—А–µ–Ј –Ї–Њ—В–Њ—А–Њ–µ –њ–µ—А–≤–є –Њ–њ–µ—А–µ–і–Є–ї –≤—В–Њ—А–Њ–≥–Њ –љ–∞ 50 –Љ.
–Ю—В–≤–µ—В: —З–µ—А–µ–Ј 25 —Б–µ–Ї—Г–љ–і.
–Э–∞–Љ —Г–ґ–µ –Ј–љ–∞–Ї–Њ–Љ—Л –Ј–∞–і–∞—З–Є, —Г—Б–ї–Њ–≤–Є—П –Є —А–µ—И–µ–љ–Є—П –Ї–Њ—В–Њ—А—Л—Е –≤–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј–∞–љ—Л. –Х—Б–ї–Є –Њ–і–љ–Њ –Є–Ј –і–∞–љ–љ—Л—Е –≤ —Г—Б–ї–Њ–≤–Є–Є –Ј–∞–і–∞—З–Є –њ–Њ—Б—З–Є—В–∞—В—М –љ–µ–Є–Ј–≤–µ—Б—В–љ—Л–Љ, –∞ –≤—Л—З–Є—Б–ї–µ–љ–љ–Њ–µ –љ–µ–Є–Ј–≤–µ—Б—В–љ–Њ–µ –≤–Ј—П—В—М –Ј–∞ –і–∞–љ–љ–Њ–µ, —В–Њ –њ–Њ–ї—Г—З–Є—В—Б—П –Ј–∞–і–∞—З–∞, –Њ–±—А–∞—В–љ–∞—П –і–∞–љ–љ–Њ–є.
–Ч–∞–њ–Є—И–µ–Љ –Ї—А–∞—В–Ї–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –Њ–±—А–∞—В–љ–Њ–є –Ј–∞–і–∞—З–Є.
–Ь–∞–ї—М—З–Є–Ї–Є –±–µ–≥—Г—В –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –≤ –Њ–і–љ–Њ–Љ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–Є
–°–Ї–Њ—А–Њ—Б—В—М –њ–µ—А–≤–Њ–≥–Њ - 8 –Љ/—Б
–°–Ї–Њ—А–Њ—Б—В—М –≤—В–Њ—А–Њ–≥–Њ - 6 –Љ/—Б
–Т—А–µ–Љ—П, —З–µ—А–µ–Ј –Ї–Њ—В–Њ—А–Њ–µ –њ–µ—А–≤—Л–є –Њ–њ–µ—А–µ–і–Є–ї –≤—В–Њ—А–Њ–≥–Њ - 25 —Б
–†–∞—Б—Б—В–Њ—П–љ–Є–µ, –љ–∞ –Ї–Њ—В–Њ—А–Њ–µ –њ–µ—А–≤—Л–є –Њ–њ–µ—А–µ–і–Є–ї –≤—В–Њ—А–Њ–≥–Њ - ?
8-6=2 (–Љ/—Б) вАУ —Б–Ї–Њ—А–Њ—Б—В—М —Г–і–∞–ї–µ–љ–Є—П.
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –љ–∞–є—В–Є —А–∞—Б—Б—В–Њ—П–љ–Є–µ –њ–Њ –Є–Ј–≤–µ—Б—В–љ—Л–Љ —Б–Ї–Њ—А–Њ—Б—В–Є –Є –≤—А–µ–Љ–µ–љ–Є, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ —Б–Ї–Њ—А–Њ—Б—В—М —Г–Љ–љ–Њ–ґ–Є—В—М –љ–∞ –≤—А–µ–Љ—П.
–£–Љ–љ–Њ–ґ–Є–Љ –≤—А–µ–Љ—П, —З–µ—А–µ–Ј –Ї–Њ—В–Њ—А–Њ–µ –њ–µ–≤—Л–є –Њ–њ–µ—А–µ–і–Є–ї –≤—В–Њ—А–Њ–≥–Њ, –љ–∞ —Б–Ї–Њ—А–Њ—Б—В—М —Г–і–∞–ї–µ–љ–Є—П.
25вИЩ2=50 (–Љ) вАУ —А–∞—Б—Б—В–Њ—П–љ–Є–µ, –љ–∞ –Ї–Њ—В–Њ—А–Њ–µ –њ–µ—А–≤—Л–є –Њ–њ–µ—А–µ–і–Є–ї –≤—В–Њ—А–Њ–≥–Њ —З–µ—А–µ–Ј 25 —Б–µ–Ї—Г–љ–і.
–Ю—В–≤–µ—В: 50 –Љ.
6.
–Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ 1 —Ж=100 –Ї–≥.
–Ґ–Њ–≥–і–∞, 57 —Ж 7 –Ї–≥=57 —Ж+7 –Ї–≥=57вИЩ1 —Ж+7 –Ї–≥=
=57вИЩ100 –Ї–≥+7 –Ї–≥=5 700 –Ї–≥+7 –Ї–≥=5 707 –Ї–≥.
5 707 –Ї–≥ < 57 070 –Ї–≥, –Ј–љ–∞—З–Є—В –Є 57 —Ж 7 –Ї–≥ < 57 070 –Ї–≥.
–Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ 1 —В=1 000 –Ї–≥.
–Ґ–Њ–≥–і–∞, 57 —В 7 –Ї–≥=57 —В+7 –Ї–≥=57вИЩ1 —В+7 –Ї–≥=
=57вИЩ1 000 –Ї–≥+7 –Ї–≥=57 000 –Ї–≥+7 –Ї–≥=57 007 –Ї–≥.
57 007 –Ї–≥=57 007 –Ї–≥, –Ј–љ–∞—З–Є—В –Є 57 —В 7 –Ї–≥=57 007 –Ї–≥.
57 –Љ–Є–љ 7 —Б < 5 770 –Љ–Є–љ
–Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ 1 –Љ=100 —Б–Љ, 1 —Б–Љ=10 –Љ–Љ, –Ј–љ–∞—З–Є—В
1 –Љ=100вИЩ10 –Љ–Љ=1 000 –Љ–Љ.
–Ґ–Њ–≥–і–∞, 57 –Љ 7 –Љ–Љ=57 –Љ+7 –Љ–Љ=57вИЩ1 –Љ+7 –Љ–Љ=
=57вИЩ1 000 –Љ–Љ+7 –Љ–Љ=57 000 –Љ–Љ+7 –Љ–Љ=57 007 –Љ–Љ.
57 007 –Љ–Љ > 5 707 –Љ–Љ, –Ј–љ–∞—З–Є—В –Є 57 –Љ 7 –Љ–Љ > 5 707 –Љ–Љ.
7.
–Ч–∞–њ–Є—И–µ–Љ –Ї—А–∞—В–Ї–Њ–µ —Г—Б–ї–Њ–≤–Є–µ –Ј–∞–і–∞—З–Є.
–Т—А–µ–Љ—П —А–∞–±–Њ—В—Л –†–∞—Б—Е–Њ–і –≥–Њ—А—О—З–µ–≥–Њ
1 —В—А–∞–Ї—В–Њ—А 60 —З–∞—Б–Њ–≤ ? –ї
2 —В—А–∞–Ї—В–Њ—А 55 —З–∞—Б–Њ–≤ ? –ї, –љ–∞ 40 –ї –Љ–µ–љ—М—И–µ, —З–µ–Љ –љ–∞ –њ–µ—А–≤–Њ–Љ
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —Г–Ј–љ–∞—В—М, –љ–∞ —Б–Ї–Њ–ї—М–Ї–Њ –Њ–і–љ–Њ —З–Є—Б–ї–Њ –±–Њ–ї—М—И–µ –Є–ї–Є –Љ–µ–љ—М—И–µ –і—А—Г–≥–Њ–≥–Њ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Є–Ј –±–Њ–ї—М—И–µ–≥–Њ —З–Є—Б–ї–∞ –≤—Л—З–µ—Б—В—М –Љ–µ–љ—М—И–µ–µ.
вАГ
–Э–∞–є–і—С–Љ, –љ–∞ —Б–Ї–Њ–ї—М–Ї–Њ —З–∞—Б–≤–Њ –±–Њ–ї—М—И–µ —А–∞–±–Њ—В–∞–ї –њ–µ—А–≤—Л–є —В—А–∞–Ї—В–Њ—А.
60-55=5 (—З) вАУ –±–Њ–ї—М—И–µ —А–∞–±–Њ—В–∞–ї –њ–µ—А–≤—Л–є —В—А–∞–Ї—В–Њ—А.
–Ъ–∞–ґ–і—Л–є —В—А–∞–Ї—В–Њ—А —А–∞—Б—Е–Њ–і—Г–µ—В –Ј–∞ 1 —З–∞—Б –Њ–і–Є–љ–∞–Ї–Њ–≤–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≥–Њ—А—О—З–µ–≥–Њ.
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –љ–∞–є—В–Є –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≥–Њ—А—О—З–µ–≥–Њ, –Є–Ј—А–∞—Б—Е–Њ–і–Њ–≤–∞–љ–љ–Њ–µ –Ј–∞ 1 —З–∞—Б, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –ї–Є—В—А–Њ–≤ –≥–Њ—А—О—З–µ–≥–Њ, –Є–Ј—А–∞—Б—Е–Њ–і–Њ–≤–∞–љ–љ–Њ–µ –њ–µ—А–≤—Л–Љ —В—А–∞–Ї—В–Њ—А–Њ–Љ, —А–∞–Ј–і–µ–ї–Є—В—М –љ–∞ –≤—А–µ–Љ—П –µ–≥–Њ —А–∞–±–Њ—В—Л.
40вИґ5=8 (–ї) вАУ —А–∞—Б—Е–Њ–і—Г–µ—В –Ї–∞–ґ–і—Л–є —В—А–∞–Ї—В–Њ—А –Ј–∞ 1 —З–∞—Б.
–Э–∞–є–і—С–Љ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≥–Њ—А—О—З–µ–≥–Њ, –Ї–Њ—В–Њ—А–Њ–µ –Є–Ј—А–∞—Б—Е–Њ–і–Њ–≤–∞–ї –њ–µ—А–≤—Л–є —В—А–∞–Ї—В–Њ—А вАУ —Г–Љ–љ–Њ–ґ–Є–Љ –≤—А–µ–Љ—П —А–∞–±–Њ—В—Л —В—А–∞–Ї—В–Њ—А–∞ –љ–∞ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≥–Њ—А—О—З–µ–≥–Њ, –Є–Ј—А–∞—Б—Е–Њ–і–Њ–≤–∞–љ–љ–Њ–µ –Ј–∞ 1 —З–∞—Б.
60вИЩ8=480 (–ї) вАУ –Є–Ј—А–∞—Б—Е–Њ–і–Њ–≤–∞–ї –њ–µ—А–≤—Л–є —В—А–∞–Ї—В–Њ—А.
–Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —Г–Љ–љ–Њ–ґ–Є—В—М –Ї—А—Г–≥–ї–Њ–µ —З–Є—Б–ї–Њ –љ–∞ –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ–µ, –Љ–Њ–ґ–љ–Њ –≤—Л–њ–Њ–ї–љ–Є—В—М —Г–Љ–љ–Њ–ґ–µ–љ–Є–µ, –љ–µ –Њ–±—А–∞—Й–∞—П –≤–љ–Є–Љ–∞–љ–Є—П –љ–∞ –љ—Г–ї–Є, –∞ –Ј–∞—В–µ–Љ –њ—А–Є–њ–Є—Б–∞—В—М —Б—В–Њ–ї—М–Ї–Њ –љ—Г–ї–µ–є, —Б–Ї–Њ–ї—М–Ї–Њ –Є—Е –≤ –Ї—А—Г–≥–ї–Њ–Љ —З–Є—Б–ї–µ.
480-40=440 (–ї) вАУ –Є–Ј—А–∞—Б—Е–Њ–і–Њ–≤–∞–ї –≤—В–Њ—А–Њ–є —В—А–∞–Ї—В–Њ—А.
–Ю—В–≤–µ—В: 480 –ї –Є 440 –ї.
9.
350-15вИЩ104-1 428вИґ14
–Т—Б–њ–Њ–Љ–љ–Є–Љ –њ–Њ—А—П–і–Њ–Ї –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П –і–µ–є—Б—В–≤–Є–є –≤ –≤—Л—А–∞–ґ–µ–љ–Є—П—Е.
- –µ—Б–ї–Є –≤ –≤—Л—А–∞–ґ–µ–љ–Є–Є –љ–µ—В —Б–Ї–Њ–±–Њ–Ї, —В–Њ —Б–љ–∞—З–∞–ї–∞ –≤—Л–њ–Њ–ї–љ—П—О—В —Г–Љ–љ–Њ–ґ–µ–љ–Є–µ –Є–ї–Є –і–µ–ї–µ–љ–Є–µ, –∞ –њ–Њ—В–Њ–Љ вАУ —Б–ї–Њ–ґ–µ–љ–Є–µ –Є–ї–Є –≤—Л—З–Є—В–∞–љ–Є–µ (—Б–ї–µ–≤–∞ –љ–∞–њ—А–∞–≤–Њ).
- –µ—Б–ї–Є –≤ –≤—Л—А–∞–ґ–µ–љ–Є–Є –µ—Б—В—М —Б–Ї–Њ–±–Ї–Є, —В–Њ —Б–љ–∞—З–∞–ї–∞ –≤—Л–њ–Њ–ї–љ—П—О—В –і–µ–є—Б—В–≤–Є—П –≤ —Б–Ї–Њ–±–Ї–∞—Е, –∞ –Ј–∞—В–µ–Љ –њ—А–Є–Љ–µ–љ—П—О—В –њ–µ—А–≤–Њ–µ –њ—А–∞–≤–Є–ї–Њ.
–Я–Њ–і—Г–Љ–∞–µ–Љ, —З—В–Њ –њ–Њ–ї—Г—З–Є–Љ –њ—А–Є –і–µ–ї–µ–љ–Є–Є 1 428 –љ–∞ 14.
1428 14
14 102
28
28
0
–Я–Є—И–µ–Љ: 1 428вИґ14.
вАГ
–Я–µ—А–≤–Њ–µ –љ–µ–њ–Њ–ї–љ–Њ–µ –і–µ–ї–Є–Љ–Њ–µ вАУ 14 —Б–Њ—В–µ–љ. –Ч–љ–∞—З–Є—В, –≤ —З–∞—Б—В–љ–Њ–Љ –±—Г–і–µ—В 3 —Ж–Є—Д—А—Л.
–Ф–µ–ї—О —Б–Њ—В–љ–Є: —А–∞–Ј–і–µ–ї—О 14 –љ–∞ 14, –њ–Њ–ї—Г—З—Г 1 - —Б—В–Њ–ї—М–Ї–Њ —Б–Њ—В–µ–љ –±—Г–і–µ—В –≤ —З–∞—Б—В–љ–Њ–Љ.
–£–Љ–љ–Њ–ґ—Г 14 –љ–∞ 1, –њ–Њ–ї—Г—З—Г 14 - —Б—В–Њ–ї—М–Ї–Њ —Б–Њ—В–µ–љ —А–∞–Ј–і–µ–ї–Є–ї–Є.
–Т—Л—З—В—Г: 14-14=0 вАУ —Б–Њ—В–љ–Є —А–∞–Ј–і–µ–ї–Є–ї–Є –≤—Б–µ.
–Ф–µ–ї—О –і–µ—Б—П—В–Ї–Є: 2 –і–µ—Б—П—В–Ї–∞ –љ–µ–ї—М–Ј—П —А–∞–Ј–і–µ–ї–Є—В—М –љ–∞ 14 —В–∞–Ї, —З—В–Њ–±—Л –≤ —З–∞—Б—В–љ–Њ–Љ –њ–Њ–ї—Г—З–Є–ї–Є—Б—М —Б–Њ—В–љ–Є, –њ–Њ—Н—В–Њ–Љ—Г –њ–Є—И–µ–Љ –≤ —З–∞—Б—В–љ–Њ–Љ 0.
–Ф–µ–ї—О –µ–і–Є–љ–Є—Ж—Л: 2 –і–µ—Б—П—В–Ї–∞ 8 –µ–і–Є–љ–Є—Ж вАУ —Н—В–Њ 28 –µ–і–Є–љ–Є—Ж.
–†–∞–Ј–і–µ–ї—О 28 –љ–∞ 14, –њ–Њ–ї—Г—З—Г 2 - —Б—В–Њ–ї—М–Ї–Њ –µ–і–Є–љ–Є—Ж –±—Г–і–µ—В –≤ —З–∞—Б—В–љ–Њ–Љ.
–£–Љ–љ–Њ–ґ—Г 14 –љ–∞ 2, –њ–Њ–ї—Г—З—Г 28 - —Б—В–Њ–ї—М–Ї–Њ –µ–і–Є–љ–Є—Ж —А–∞–Ј–і–µ–ї–Є–ї–Є.
–Т—Л—З—В—Г: 28-28=0 вАУ –µ–і–Є–љ–Є—Ж—Л —А–∞–Ј–і–µ–ї–Є–ї–Є –≤—Б–µ.
–І–Є—В–∞—О –Њ—В–≤–µ—В: 102.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –≤—Л—А–∞–ґ–µ–љ–Є–µ –Є–Ј —Г—Б–ї–Њ–≤–Є—П —Б —Г—З—С—В–Њ–Љ –≤—Л–њ–Њ–ї–љ–µ–љ–љ–Њ–≥–Њ –і–µ–ї–µ–љ–Є—П.
350-15вИЩ104-1 428вИґ14=350-15вИЩ104-102
–Я–Њ–і—Г–Љ–∞–µ–Љ, –Ї–∞–Ї —А–∞—Б—Б—В–∞–≤–Є—В—М —Б–Ї–Њ–±–Ї –≤ –≤—Л—А–∞–ґ–µ–љ–Є–Є.
–Х—Б–ї–Є –Є–Ј 104 –≤—Л—З–µ—Б—В—М 102, –њ–Њ–ї—Г—З–Є–Љ 2.
–Ґ–Њ–≥–і–∞, –њ—А–Є —Г–Љ–љ–Њ–ґ–µ–љ–Є–Є 15 –љ–∞ 2, –њ–Њ–ї—Г—З–Є–Љ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ 30.
–Р –њ—А–Є –≤—Л—З–Є—В–∞–љ–Є–Є 350-30 –њ–Њ–ї—Г—З–Є–Љ —А–∞–Ј–љ–Њ—Б—В—М 320.
–Ґ–Њ–≥–і–∞, —Б–ї–µ–і—Г–µ—В —А–∞—Б—Б—В–∞–≤–Є—В—М —Б–Ї–Њ–±–Ї–Є —В–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
350-15вИЩ(104-102)
–†–∞—Б—Б—В–∞–≤–Є–Љ —Б–Ї–Њ–±–Ї–Є –≤ –≤—Л—А–∞–ґ–µ–љ–Є–Є –Є–Ј —Г—Б–ї–Њ–≤–Є—П
350-15вИЩ(104-1 428вИґ14).
ѕохожие решебники
ѕопул€рные решебники 4 класс ¬се решебники
* сожалению, временные проблемы с публикацией комментариев с мобильных устройств.