Стр.7 Часть 2 ГДЗ Дорофеев Миракова 4 класс (Математика)
Решение #1


Решение #2









Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
2. За телевизор заплатили 65 070 р., а за холодильник — на 38 690 р. меньше. Сколько стоит холодильник?
3. На участке дороги длиной 12 630 м работали две бригады ремонтников. Первая бригада уже отремонтировала 4 375 м дороги, а вторая бригада — на 816 м меньше. Сколько метров дороги осталось отремонтировать?
4. Вырази в метрах или в метрах и дециметрах:
380 дм; 275 дм; 600 см; 940 см; 1 000 дм.
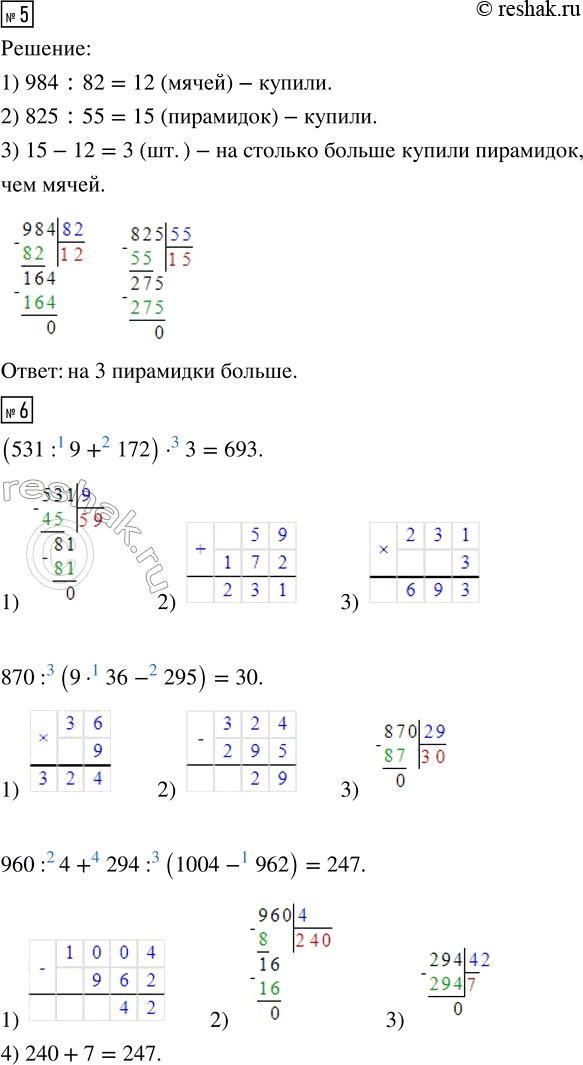
5. Для детского сада купили мячи на 984 р., по 82 р. за мяч, и пирамидки на 825 р., по 55 р. за штуку. Каких игрушек купили больше: мячей или пирамидок — и на сколько больше?
6. Выполни действия.
(531 : 9 + 172) · 3 960 : 4 + 294 : (1 004 - 962)
870 : (9 · 36 - 295) 450 : 5 - (630 : 7 - 810 : 9)
7. Длина одной доски 8 м, ширина 25 см; длина другой доски 9 м, ширина 20 см. На сколько квадратных сантиметров площадь одной доски больше, чем площадь другой?
8. Можно ли из проволоки длиной 180 мм путём перегибания изготовить равносторонний треугольник, длина стороны которого равна 58 мм? Останется ли ещё проволока? Если останется, то какой длины?
2.
Составим краткое условие задачи.
Телевизор - 65 070 рублей
Холодильник - ? рублей, на 38 690 рублей меньше
Задача решается вычитанием: 65 070-38 690.
Вспомним правило вычитания многозначных чисел – при вычитании многозначных чисел столбиком вычитают единицы из единиц, десятки из десятков, и так далее.
65 070
38 690
26 380
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч): 65 070-38 690.
Вычитаем единицы: 0-0=0. Пишем 0 под единицами.
Вычитаем десятки: из 7 дес. нельзя вычесть 9 дес., из 0 сот. занять нельзя, поэтому возьмём из 5 ед. тысяч 1 ед. тыс., то есть 10 сотен (для того, чтобы не забыть, ставим точку над цифрой 5). Распределим 10 сотен, как 9 сотен и 10 десятков. 10+7=17.
Вычтем: 17-9=8. Пишем 8 под десятками.
Вычитаем сотни: сотен было 0, но после того, как заняли 1 единицу тысяч при вычитании десятков, осталось 9 сотен.
9-6=3. Пишем 3 под сотнями.
Вычитаем единицы тысяч: из 5 единиц тысяч мы взяли 1 единицу тысяч при вычитании десятков, осталось 4 единицы тысяч.
Из 4 ед. тыс. нельзя вычесть 8 ед. тысяч, поэтому возьмём из 6 десятков тысяч 1 десяток тысяч, то есть 10 единиц тысяч (для того, чтобы не забыть, ставим точку над цифрой 6). 10+4=14.
Вычтем: 14-8=6. Пишем 6 под единицами тысяч.
Вычитаем десятки тысяч: из 6 десятков тысяч мы взяли 1 десяток тысяч при вычитании единиц тысяч, осталось 5 десятков тысяч.
5-3=2. Пишем 2 под десятками тысяч.
Читаем ответ: 26 380.
Значит, холодильник стоит 26 380 рублей.
Ответ: 26 380 рублей.
3.
Составим краткое условие задачи.
1 бригада - 4 375 м
2 бригада - ? м, на 816 м меньше
Осталось - ? м
Всего - 12 630 м
Найдём длину участка дороги, который отремонтировала вторая бригада: 4 375-816.
Вспомним правило вычитания многозначных чисел - при вычитании многозначных чисел столбиком вычитают единицы из единиц, десятки из десятков, и так далее.
4 375
816
3 559
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 4 375-816.
Вычитаем единицы: из 5 единиц нельзя вычесть 6 единиц, поэтому возьмём из 7 десятков 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 7). 10+5=15.
15-6=9. Пишем 9 под единицами.
Вычитаем десятки: из 7 десятков взяли 1 десяток при вычитании единиц, осталось 6 десятков.
6-1=5. Пишем 5 под десятками.
Вычитаем сотни: из 3 сотен нельзя вычесть 8 сотен, поэтому возьмём из 4 единиц тысяч 1 единицу тысяч, то есть 10 сотен (для того, чтобы не забыть, ставим точку над цифрой 4). 10+3=13.
13-8=5. Пишем 5 под сотнями.
Единиц тысяч было 4, но 1 единицу тысяч взяли при вычитании сотен, осталось 3 единицы тысяч.
Читаем ответ: 3 559.
Значит, вторая бригада отремонтировала 3 559 м дороги.
Найдём, сколько метров дороги отремонтировали две бригады вместе: 4 375+3 559.
4 375
3 559
7 934
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, тысячи под тысячами): 4 375+3 559.
Складываю единицы: 5+9=14. 14 ед. - это 1 дес. и 4 ед.; пишу 4 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Складываю десятки: 7+5=12, да ещё 1.
12+1=13. 13 дес. – это 1 сот. 3 дес.; пишу 3 под десятками, а 1 сотню запомню и прибавлю к сотням.
Складываю сотни: 3+5=8, да ещё 1.
8+1=9. Пишу 9 под сотнями.
Складываю тысячи: 4+3=7. Пишу 7 под тысячами.
Читаю ответ: 7 934.
Значит, отремонтировано 7 934 м дороги.
Для того, чтобы определить сколько метров дороги осталось отремонтировать, необходимо из всего участка дороги вычесть отремонтированный двумя бригадами участок дороги:
12 630-7 934.
12 630
7 934
4 696
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, тысячи под тысячами): 12 630-7 934.
Вычитаем единицы: из 0 единиц нельзя вычесть 4 единицы, поэтому возьмём из 3 десятков 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 3). 10+0=10.
10-4=6. Пишем 6 под единицами.
Вычитаем десятки: из 3 десятков взяли 1 десяток при вычитании единиц, осталось 2 десятка.
Из 2 десятков нельзя вычесть 3 десятка, поэтому возьмём из 6 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 6). 10+2=12.
Вычтем: 12-3=9. Пишем 9 под десятками.
Вычитаем сотни: сотен было 6, но после того, как заняли 1 сотню при вычитании десятков, осталось 5 сотен.
Из 5 сот. нельзя вычесть 9 сот., поэтому возьмём из 2 ед. тыс. 1 ед. тыс., то есть 10 сот. (для того, чтобы не забыть, ставим точку над цифрой 2). 10+5=15.
Вычтем: 15-9=6. Пишем 6 под сотнями.
Вычитаем единицы тысяч: ед. тыс. было 2, но после того, как заняли 1 ед. тыс. при вычитании сотен, осталась 1 единица тысяч.
Из 1 ед. тысяч нельзя вычесть 7 единиц тысяч, поэтому возьмём из 1 десятка тысяч 1 десяток тысяч, то есть 10 единиц тысяч (для того, чтобы не забыть, ставим точку над цифрой 1). 10+1=11.
Вычтем: 11-7=4. Пишем 4 под единицами тысяч.
Из 1 десятка тысяч мы взяли 1 десяток тысяч при вычитании единиц тысяч, осталось 0 десятков тысяч.
Ноль на месте высшего разряда принято не писать.
Читаем ответ: 4 696.
Значит, осталось отремонтировать 4 696 м дороги.
Ответ: 4 696 м.
4.
Вспомним, сколько дециметров в одном метре.
1 м=10 дм.
Тогда, 380 дм=38•10 дм=38•1 м=38 м.
275 дм=270 дм+5 дм=27•10 дм+5 дм=27•1 м+5 дм==27 м+5 дм=27 м 5 дм.
Вспомним, сколько см в одном метре и сколько см в одном дм.
1 м=100 см, 1 дм=10 см.
Тогда, 600 см=6•100 см=6•1 м=6 м.
940 см=900 см+40 см=9•100 см+4•10 см=
=9•1 м+4•1 дм=9 м+4 дм=9 м 4 дм.
1 000 дм=100•10 дм=100•1 м=100 м.
5.
Составим краткое условие задачи.
Мячи - ? шт. по 82 р., всего 984 р.
Пирамидки - ? шт. по 55 р., всего 825 р.
Больше - ?, на ? шт.
Мячей купили на 984 рубля по 82 рубля за штуку.
Для того, чтобы узнать стоимость одной штуки, необходимо разделить 984 на 82.
984
82
82 12
164
164
0
Пишем: 984:82.
Первое неполное делимое – 98 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 98 на 82, получу 1 - столько десятков будет в частном.
Умножу 82 на 1, получу 82 - столько десятков разделили.
Вычту: 98-82=16 – столько десятков осталось разделить.
Делим единицы: 16 десятков 4 единицы – это 164 единицы.
Разделю 164 на 82, получу 2 - столько единиц будет в частном.
Умножу 82 на 2, получу 164 - столько единиц разделили.
Вычту: 164-164=0 – единицы разделили все.
Читаю ответ: 12.
Значит, купили 12 мячей.
Пирамидок купили на 825 рублей по 55 рублей за штуку.
Для того, чтобы узнать стоимость одной штуки, необходимо разделить 825 на 55.
825
55
55 15
275
275
0
Пишем: 825:55.
Первое неполное делимое – 82 десятка. Значит, в частном будет 2 цифры.
Делю десятки: разделю 82 на 55, получу 1 - столько десятков будет в частном.
Умножу 55 на 1, получу 55 - столько десятков разделили.
Вычту: 82-55=27 – столько десятков осталось разделить.
Делим единицы: 27 десятков 5 единиц – это 275 единиц.
Разделю 275 на 55, получу 5 - столько единиц будет в частном.
Умножу 55 на 5, получу 275 - столько единиц разделили.
Вычту: 275-275=0 – единицы разделили все.
Читаю ответ: 15.
Значит, купили 15 пирамидок.
Так как 12 < 15, то пирамидок купили больше.
Узнаем, на сколько больше купили пирамидок.
15-12=3 (шт).
Значит, пирамидок купили больше на 3 штуки.
Ответ: пирамидок купили больше на 3 штуки.
6.
Вспомним порядок действий в выражении:
- если в выражении нет скобок, и оно содержит действия обоих ступеней, то сначала выполняют действия второй ступени (умножение и деление), а потом действия первой ступени (сложение и вычитание).
- если в выражении есть скобки (одна или несколько пар), то сначала выполняют действия в скобках, а потом все остальные действия по пункту 1.
1 2 3
(531:9+172)•3=(59+172)•3=231•3=693
3 1 2
870:(9•36-295)=870:(324-295)=870:29=30
2 4 3 1
960:4+294:(1 004-962)=960:4+294:42=
=240+294:42=240+7=247
4 5 1 3 2
450:5-(630:7-810:9)=450:5-(90-810:9)=
=450:5-(90-90)=450:5-0=90-0=90
7.
Запишем краткое условие задачи.
Длина Ширина Площадь
1 доска 8 м 25 см ?
2 доска 9 м 20 см ?
Вспомним, сколько сантиметров в одном метре: 1 м=100 см.
Переведём все значения в одинаковые единицы измерения.
Длина первой доски: 8 м=8•1 м=8•100 см=800 см.
Длина второй доски: 9 м=9•1 м=9•100 см=900 см.
Для того, чтобы найти площадь прямоугольника, необходимо умножить его длину на ширину.
Найдём площадь первой доски, умножив 800 на 25.
800•25=20 000 (?см?^2) - площадь первой доски.
Найдём площадь второй доски, умножив 900 на 20.
900•20=18 000 (?см?^2) - площадь второй доски.
Для того, чтобы найти, на сколько площадь одной доски больше площади другой доски, необходимо из площади одной доски вычесть площадь другой доски.
Вычтем 18 000 из 20 000:
20 000-18 000=2 000 (?см?^2) – на столько площадь первой доски больше площади второй доски.
Ответ: на 2 000 ?см?^2.
8.
Запишем краткое условие задачи.
Длина проволоки 180 мм
Длина стороны треугольника 58 мм
Можно ли изготовить равносторонний треугольник ?
Останется ли проволока, если да, то сколько ?
Вычислим, сколько мм проволоки понадобится, чтобы изготовить треугольник.
Для этого умножим длину стороны треугольника 58 мм на количество сторон треугольника 3.
58•3=174 (мм) – проволоки понадобится для треугольника.
Для того, чтобы понять, хватит ли проволоки для изготовления треугольника, необходимо сравнить сколько мм проволоки у нас есть и сколько мм проволоки нам понадобится.
Если у нас есть больше или столько же мм проволоки, сколько необходимо для треугольника, значит, мы сможем его изготовить.
Если у нас меньше мм проволоки, чем необходимо для треугольника, значит, мы не сможем его изготовить.
У нас есть 180 мм проволоки.
Для изготовления треугольника необходимо 174 мм проволоки.
180 мм > 174 мм, значит, мы сможем изготовить треугольник.
Для того, чтобы узнать, сколько мм проволоки останется, необходимо вычесть из длины всей проволоки длину проволоки, которая необходима для изготовления треугольника.
180-174=6 (мм) – проволоки останется.
Ответ: можно изготовить треугольник; останется 6 мм проволоки.
Похожие решебники
Популярные решебники 4 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.