Стр.91 Часть 1 ГДЗ Дорофеев Миракова 4 класс (Математика)
Решение #1

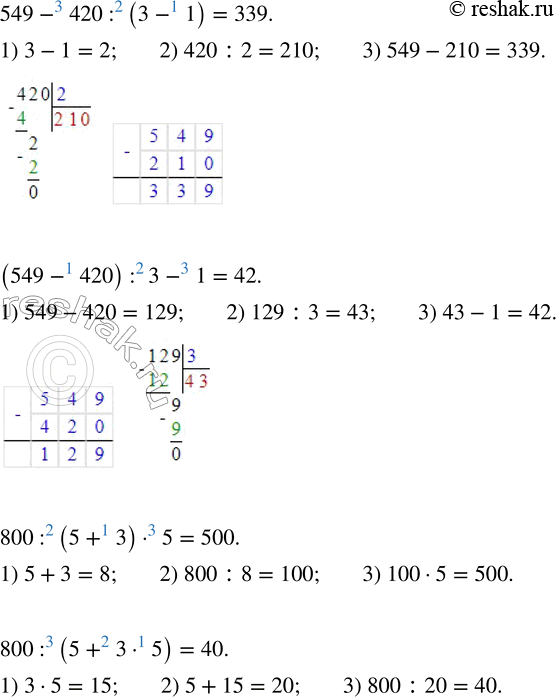

Решение #2





Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
15. Скорый поезд прошёл 320 км со скоростью 80 км/ч. Товарный поезд прошёл за это же время 200 км. С какой скоростью шёл товарный поезд?
Запишем краткое условие задачи.
Расстояние, которое прошёл скорый поезд - 320 км
Скорость скорого поезда - 80 км/ч
Расстояние, которое прошёл товарный поезд - 200 км
Скорость товарного поезда - ? км/ч
Время в пути - одинаковое
Для того, чтобы найти время по известным расстоянию и скорости, необходимо расстояние разделить на скорость.
Известно, что скорый поезд прошёл 320 км со скоростью 80 км/ч. Значит, чтобы найти его время в пути, необходимо 320 разделить на 80: 320:80.
Представим делитель 80, как произведение чисел 10 и 8. Тогда получим выражение 320:(10•8).
Воспользуемся правилом деления числа на произведение: сначала разделим 320 на 10, получим 32, а потом это число разделим на 8. В ответе получится 4.
320:80=320:(10•8)=320:10:8=32:8=4
Значит, скорый поезд был в пути 4 часа.
Для того, чтобы найти скорость по известному расстоянию и времени, необходимо расстояние разделить на время.
Известно, что товарный поезд потратил столько же времени, как и скорый поезд, то есть 4 часа. Также известно, что товарный поезд прошёл за это время 200 км. Значит, чтобы найти скорость товарного поезда, необходимо 200 разделить на 4.
200:4=20 дес.:4=5 дес.=50 (км/ч) – скорость товарного поезда.
Ответ: 50 км/ч.
16. Сравни, не проводя вычислений полностью. Объясни, какие свойства действий можно использовать для сравнения значений выражений.
500 · 3 + 500 · 2 и 500 · 4 81 : 9 + 45 : 9 и 126 : 9
140 · 4 - 140 · 2 и 140 · 2 125 · 6 - 125 · 2 и 125 · 3
17. Расставь скобки так, чтобы получились верные записи.
549 - 420 : 3 - 1 = 410 800 : 5 + 3 · 5 = 500
549 - 420 : 3 - 1 = 339 800 : 5 + 3 · 5 = 40
549 - 420 : 3 - 1 = 42 800 : 5 + 3 · 5 = 815
Если в выражении есть скобки, то сначала выполняют действия в скобках, а потом все остальные действия: сначала действия второй ступени (умножение и деление), а потом действия первой ступени (сложение и вычитание).
В первой тройке примеров необходимо проставить скобки в выражении 549-420:3-1.
Рассмотрим первый вариант расположения скобок в выражении.
(549-420) :3-1=129:3-1=43-1=42
129
3
12 43
9
9
0
Пишем: 129:3.
Первое неполное делимое – 12 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 12 на 3, получу 4 – столько десятков будет в частном.
Умножу 3 на 4, получу 12 – столько десятков разделили.
Вычту: 12-12=0 – десятки разделили все.
Делю единицы: разделю 9 на 3, получу 3 – столько единиц будет в частном.
Умножу 3 на 3, получу 9 – столько единиц разделили.
Вычту: 9-9=0 – единицы разделили все.
Читаю ответ: 43.
Значит, вариант расположения скобок (549-420) :3-1 подходит для примера 3.
Рассмотрим второй вариант расположения скобок в выражении.
549-420:(3-1)=549-420:2=549-(400+20) :2=549-(400:2+20:2)=549-(200+10)=549-210=339
Значит, вариант расположения скобок 549-420:(3-1) подходит для примера 2.
Рассмотрим третий вариант расположения скобок в выражении.
549-(420:3-1)=549-((300+120) :3-1)=549-((300:3+120:3)-1)=549-((100+40)-1)=549-(140-1)=549-139=410
Значит, вариант расположения скобок 549-(420:3-1) подходит для примера 1.
Рассмотрим вторую тройку примеров.
Для второй тройки примеров необходимо проставить скобки в выражении 800:5+3•5.
Рассмотрим первый вариант расположения скобок.
800:(5+3•5)=800:(5+15)=800:20=800:20=80:2=40
Значит, вариант расположения скобок 800:(5+3•5) подходит для примера 5.
Рассмотрим второй вариант расположения скобок в выражении.
(800:5+3)•5=(160+3)•5=163•5=815
800
5
5 160
30
30
0
Пишем: 800:5.
Первое неполное делимое – 8 сотен. Значит, в частном будет 3 цифры.
Делю сотни: разделю 8 на 5, получу 1 – столько сотен будет в частном.
Умножу 5 на 1, получу 5 – столько сотен разделили.
Вычту: 8-5=3 – столько десятков осталось разделить.
Делю десятки: 3 десятка 0 единиц – это 30 единиц.
Разделю 30 на 5, получу 6 – столько десятков будет в частном.
Умножу 5 на 6, получу 30 – столько десятков разделили.
Вычту: 30-30=0 – десятки разделили все.
Осталось 0 единиц, поэтому пишем в частном 0, так как при делении 0 на любое число, получится 0.
Читаю ответ: 160.
163
5
815
Пишу: 163•5.
Умножаю единицы: 3•5=15. 15 ед. – это 1 дес. 5 единиц; пишу 5 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Умножаю десятки: 6•5=30, да ещё 1.
30+1=31. 31 десяток – это 3 сотни 1 десяток; пишу 1 под десятками, а 3 сотни запомню и прибавлю к сотням.
Умножаю сотни: 1•5=5, да ещё 3.
5+3=8. Пишу 8 под сотнями.
Читаю ответ: 815.
Значит, вариант расположения скобок (800:5+3)•5 подходит для примера 6.
Рассмотрим третий вариант расположения скобок.
800:(5+3)•5=800:8•5=100•5=500
Значит, вариант расположения скобок 800:(5+3)•5 подходит для примера.
18. Среди данных треугольников найди равнобедренные. Назови их обозначения. Есть ли на чертеже равносторонние треугольники? А разносторонние? Если есть, запиши их обозначения.
Сколько прямых углов на чертеже? Запиши их обозначения.
19. Огород прямоугольной формы надо обнести сеткой-рабицей. Длина огорода 250 м, ширина 155 м. На расстоянии 5 м вбивают по 3 столба. Сколько столбов потребуется для этой изгороди?
Сделаем рисунок к задаче.
В первую очередь необходимо найти периметр прямоугольника, чтобы понять, сколько метров сетки-рябицы требуется для изгороди. После этого можно будет вычислить количество столбов.
Периметр прямоугольника – это сумма всех его сторон.
250+250+155+155=2•250+2•155=2•(200+50)+2•(150+5)=2•200+2•50+2•150+2•5=400+100+300+10=500+300+10=800+10=810 (м) – периметр изгороди.
На каждые 5 метров вбивают 3 столба. Значит, необходимо длину изгороди разделить на 5, чтобы узнать, сколько участков по 5 метров будет в изгороди.
810:5=(500+300+10) :5=500:5+300:5+10:5=100+60+2=160+2=162 – изгородь можно разделить на 162 части по 5 метров.
Так как на каждую часть изгороди по 5 метров вбивается по 3 столба, а таких участков 162, то для того, чтобы вычислить общее количество столбов, необходимо 162 умножить на 3.
162
3
486
Пишу: 162•3.
Умножаю единицы: 2•3=6. Пишу 6 под единицами.
Умножаю десятки: 6•3=18. 18 дес. – это 1 сотня 8 десятков; пишу 8 под десятками, а 1 сотню запомню и прибавлю к сотням.
Умножаю сотни: 1•3=3, да ещё 1.
3+1=4. Пишу 4 под сотнями.
Читаю ответ: 486.
Значит, 486 столбов потребуется для изгороди.
Ответ: 486 столбов.
Похожие решебники
Популярные решебники 4 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.