Стр.82 Часть 1 ГДЗ Дорофеев Миракова 4 класс (Математика)
Решение #1


Решение #2










Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
6. Выполни действия.
320 - 306 : 6 610 - 497 : 7 + 48 (700 - 285 : 3 · 4) : 2
536 : (68 : 17) (150 - 125 : 5) · 8 27 · (840 : 7 - 19 · 6)
Действия в числовых выражениях выполняются в следующем порядке:
- действия, записанные в скобках;
- умножение и деление;
- сложение и вычитание.
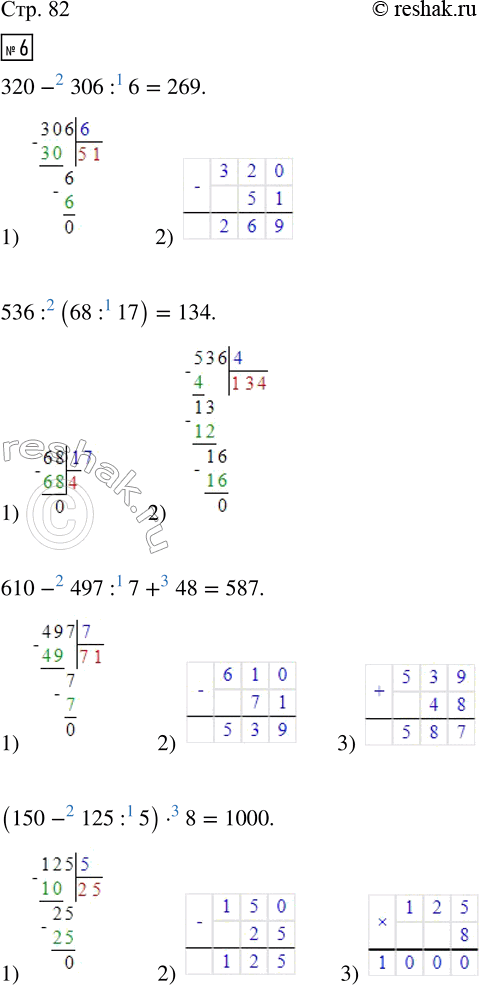
320-306:6=320-51=269
306
6
30 51
6
6
0
Пишем: 306:6.
Первое неполное делимое – 30 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 30 на 6, получу 5 – столько десятков будет в частном.
Умножу 6 на 5, получу 30 – столько десятков разделили.
Вычту: 30-30=0 – десятки разделили все.
Делю единицы: разделю 6 на 6, получу 1 – столько единиц будет в частном.
Умножу 6 на 1, получу 6 – столько единиц разделили.
Вычту: 6-6=0 – единицы разделили все.
Читаю ответ: 51.
320
51
269
Пишу (единицы под единицами, десятки под десятками):
320-51.
Вычитаем единицы: из 0 единиц нельзя вычесть 1 единицу, поэтому возьмём из 2 десятков 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 2). 10+0=10.
Вычтем: 10-1=9. Пишу 9 под единицами.
Вычитаем десятки: было 2 дес., но после того, как заняли 1 дес. при вычитании ед., остался 1 дес. Из 1 дес. нельзя вычесть 5 дес., поэтому возьмём из 3 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 3). 10+1=11.
Вычтем: 11-5=6. Пишем 6 под десятками.
Было 3 сотни, но после того, как 1 сотню заняли при вычитании десятков, осталось 2 сотни. Спускаем в ответ 2 сотни.
Читаем ответ: 269.
536:(68:17)=536:4=134
536
4
4 134
13
12
16
16
0
Пишем: 536:4.
Первое неполное делимое – 5 сотен. Значит, в частном будет 3 цифры.
Делю сотни: разделю 5 на 4, получу 1 – столько сотен будет в частном.
Умножу 4 на 1, получу 4 – столько сотен разделили.
Вычту: 5-4=1 – столько сотен осталось разделить.
Делю десятки: 1 сотня 3 десятка – это 13 десятков.
Разделю 13 на 4, получу 3 – столько десятков будет в частном.
Умножу 4 на 3, получу 12 – столько десятков разделили.
Вычту: 13-12=1 – столько десятков осталось разделить.
Делю единицы: 1 десяток 6 единиц – это 16 единиц.
Разделю 16 на 4, получу 4 – столько единиц будет в частном.
Умножу 4 на 4, получу 16 – столько единиц разделили.
Вычту: 16-16=0 – единицы разделили все.
Читаю ответ: 134.
610-497:7+48=610-71+48=539+48=587
497
7
49 71
7
7
0
Пишем: 497:7.
Первое неполное делимое – 49 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 49 на 7, получу 7 – столько десятков будет в частном.
Умножу 7 на 7, получу 49 – столько десятков разделили.
Вычту: 49-49=0 – десятки разделили все.
Делю единицы: разделю 7 на 7, получу 1 – столько единиц будет в частном.
Умножу 7 на 1, получу 7 – столько единиц разделили.
Вычту: 7-7=0 – единицы разделили все.
Читаю ответ: 71.
610
71
539
Пишу (единицы под единицами, десятки под десятками):
610-71.
Вычитаем единицы: из 0 единиц нельзя вычесть 1 единицу, поэтому возьмём из 1 десятка 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 1). 10+0=10.
Вычтем: 10-1=9. Пишу 9 под единицами.
Вычитаем десятки: был 1 дес., но после того, как заняли 1 дес. при вычитании ед., осталось 0 дес. Из 0 дес. нельзя вычесть 7 дес., поэтому возьмём из 6 сот. 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 6). 10+0=10.
Вычтем: 10-7=3. Пишем 3 под десятками.
Было 6 сотен, но после того, как 1 сотню заняли при вычитании десятков, осталось 5 сотен. Спускаем в ответ 5 сотен.
Читаем ответ: 539.
539
48
587
Пишу (единицы под единицами, десятки под десятками):
539+48.
Складываем единицы: 9+8=17. 17 ед. – это 1 дес. 7 ед.; пишу 7 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Складываем десятки: 3+4=7, да ещё 1.
7+1=8. Пишу 8 под десятками.
Спускаем в ответ 5 сотен.
Читаю ответ: 587.
(150-125:5)•8=(150-25)•8=125•8=1 000
125
5
10 25
25
25
0
Пишем: 125:5.
Первое неполное делимое – 12 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 12 на 5, получу 2 – столько десятков будет в частном.
Умножу 5 на 2, получу 10 – столько десятков разделили.
Вычту: 12-10=2 – столько десятков осталось разделить.
Делю единицы: 2 десятка 5 единиц – это 25 единиц.
Разделю 25 на 5, получу 5 – столько единиц будет в частном.
Умножу 5 на 5, получу 25 – столько единиц разделили.
Вычту: 25-25=0 – единицы разделили все.
Читаю ответ: 25.
150
25
125
Пишу (единицы под единицами, десятки под десятками):
150-25.
Вычитаем единицы: из 0 единиц нельзя вычесть 5 единиц, поэтому возьмём из 5 десятков 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 5). 10+0=10.
Вычтем: 10-5=5. Пишу 5 под единицами.
Вычитаем десятки: было 5 десятков, но после того, как заняли 1 десяток при вычитании единиц, осталось 4 десятка.
Вычтем: 4-2=2. Пишем 2 под десятками.
Спускаем в ответ 1 сотню.
Читаем ответ: 125.
125
8
1000
Пишу: 125•8.
Умножаю единицы: 5•8=40. 40 ед. – это 4 дес. 0 единиц; пишу 0 под единицами, а 4 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 2•8=16, да ещё 4.
16+4=20. 20 дес. – это 2 сотни 0 десятков; пишу 0 под десятками, а 2 сотни запомню и прибавлю к сотням.
Умножаю сотни: 1•8=8, да ещё 2.
8+2=10. 10 сот. – это 1 тыс. 0 сот.; пишу 0 под сот., а 1 тысячу пишу под тысячами, так как других тысяч для умножения нет.
Читаю ответ: 1 000.
(700-285:3•4) :2=(700-95•4) :2=(700-380) :2=320:2=160
285
3
27 95
15
15
0
Пишем: 285:3.
Первое неполное делимое – 28 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 28 на 3, получу 9 – столько десятков будет в частном.
Умножу 3 на 9, получу 27 – столько десятков разделили.
Вычту: 28-27=1 – столько десятков осталось разделить.
Делю единицы: 1 десяток 5 единиц – это 15 единиц.
Разделю 15 на 3, получу 5 – столько единиц будет в частном.
Умножу 3 на 5, получу 15 – столько единиц разделили.
Вычту: 15-15=0 – единицы разделили все.
Читаю ответ: 95.
95
4
380
Пишу: 95•4.
Умножаю единицы: 5•4=20. 20 ед. – это 2 дес. 0 единиц; пишу 0 под единицами, а 2 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 9•4=36, да ещё 2.
36+2=38. 38 дес. – это 3 сот. 8 дес.; пишу 8 под дес., а 3 сотни пишу под сотнями, так как других сотен для умножения нет.
Читаю ответ: 380.
700
380
320
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 700-380.
Вычитаем единицы: 0-0=0. Пишу 0 под единицами.
Вычитаем десятки: из 0 десятков нельзя вычесть 8 десятков, поэтому возьмём из 7 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 7). 10+0=10. Вычтем: 10-8=2. Пишем 2 под десятками.
Вычитаем сотни: было 7 сотен, но после того, как 1 сотню заняли при вычитании десятков, осталось 6 сотен.
Вычтем: 6-3=3. Пишем 3 под сотнями.
Читаем ответ: 320.
27•(840:7-19•6)=27•(120-19•6)=27•(120-114)==27•6=162
840
7
7 120
14
14
0
Пишем: 840:7.
Первое неполное делимое – 8 сотен. Значит, в частном будет 3 цифры.
Делю сотни: разделю 8 на 7, получу 1 – столько сотен будет в частном.
Умножу 7 на 1, получу 7 – столько сотен разделили.
Вычту: 8-7=1 – столько сотен осталось разделить.
Делю десятки: 1 сотня 4 десятка – это 14 десятков.
Разделю 14 на 7, получу 2 – столько десятков будет в частном.
Умножу 7 на 2, получу 14 – столько десятков разделили.
Вычту: 14-14=0 – десятки разделили все.
Осталось 0 единиц, поэтому пишем в частном 0, так как при делении 0 на любое число, получится 0.
Читаю ответ: 120.
19•6=(10+9)•6=10•6+9•6=60+54=60+(50+4)==60+50+4=(60+50)+4=110+4=114
27
6
162
Пишу: 27•6.
Умножаю единицы: 7•6=42. 42 ед. – это 4 дес. 2 ед.; пишу 2 под единицами, а 4 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 2•6=12, да ещё 4.
12+4=16. 16 дес. – это 1 сот. 6 дес.; пишу 6 под дес., а 1 сотню пишу под сотнями, так как других сотен для умножения нет.
Читаю ответ: 162.
7. Заполни пропуски в таблице, выполнив вычисления.
Сравни результаты в третьей и четвёртой строках таблицы. Какой вывод можно сделать? При каких размерах прямоугольник имеет наибольшую площадь? Как называется такой прямоугольник?
Для того, чтобы найти ширину прямоугольника, необходимо из периметра вычесть удвоенную длину прямоугольника и полученное число разделить на 2.
28•2=(20+8)•2=20•2+8•2=40+16=56
100
56
44
Пишу (единицы под единицами, десятки под десятками):
100-56.
Вычитаем единицы: из 0 ед. нельзя вычесть 6 ед., из 0 дес. занять нельзя, поэтому возьмём из 1 сот. 1 сот., то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 1). Распределим 10 десятков, как 9 десятков и 10 единиц. 10+0=10.
Вычтем: 10-6=4. Пишу 4 под единицами.
Вычитаем десятки: было 0 десятков, но после того, как при вычитании единиц заняли 1 сотню, осталось 9 десятков.
Вычтем: 9-5=4. Пишем 4 под десятками.
Была 1 сот., но после того, как при вычитании ед. заняли 1 сотню, осталось 0 сотен. 0 под высшим разрядом принято не писать.
Читаем ответ: 44.
44:2=(40+4) :2=40:2+4:2=20+2=22 (дм) – ширина.
Для того, чтобы найти площадь прямоугольника, необходимо умножить длину на ширину.
28
22
56
56
616
Пишу: 28•22.
Умножу первый множитель на число единиц: 28•2=56.
Получу первое неполное произведение: 56.
Умножу первый множитель на число десятков: 28•2=56.
Получу второе неполное произведение: 56 десятков.
Начну подписывать второе неполное произведение под десятками. Сложу неполные произведения.
Читаю ответ: 616. Это произведение чисел 28 и 22.
Значит, площадь прямоугольника равна 616 дм2.
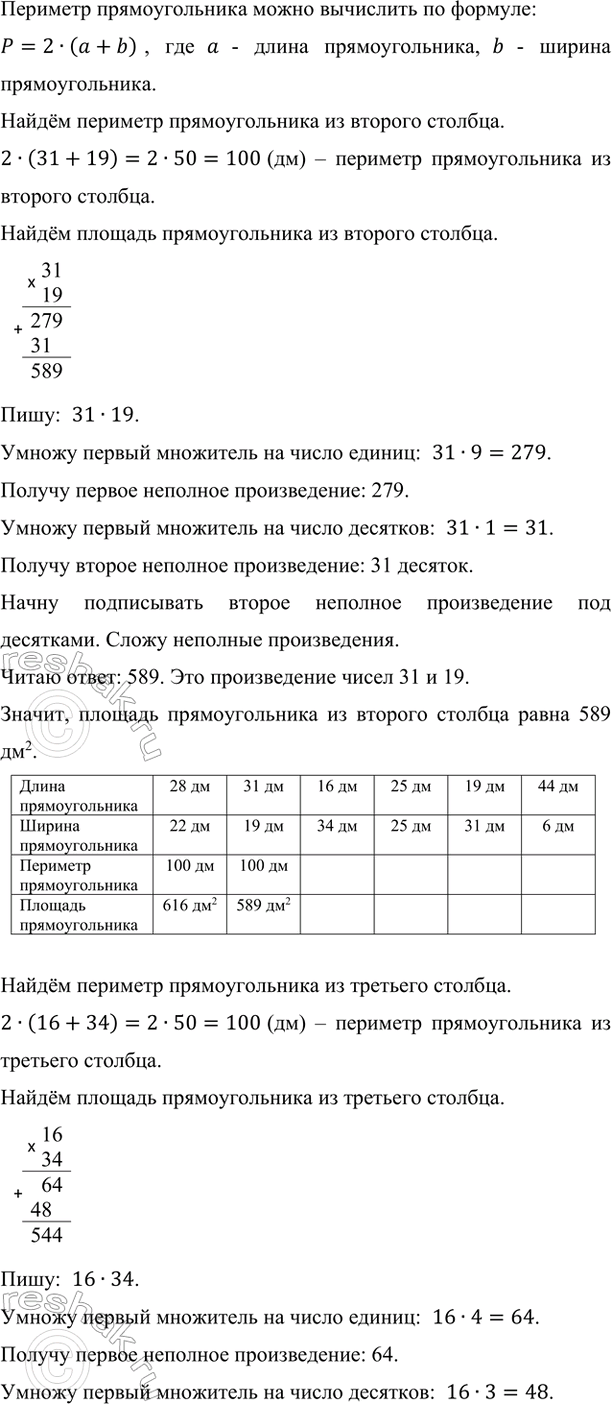
Периметр прямоугольника можно вычислить по формуле:
P=2•(a+b), где a - длина прямоугольника, b - ширина прямоугольника.
Найдём периметр прямоугольника из второго столбца.
2•(31+19)=2•50=100 (дм) – периметр прямоугольника из второго столбца.
Найдём площадь прямоугольника из второго столбца.
31
19
279
31
589
Пишу: 31•19.
Умножу первый множитель на число единиц: 31•9=279.
Получу первое неполное произведение: 279.
Умножу первый множитель на число десятков: 31•1=31.
Получу второе неполное произведение: 31 десяток.
Начну подписывать второе неполное произведение под десятками. Сложу неполные произведения.
Читаю ответ: 589. Это произведение чисел 31 и 19.
Значит, площадь прямоугольника из второго столбца равна 589 дм2.
Найдём периметр прямоугольника из третьего столбца.
2•(16+34)=2•50=100 (дм) – периметр прямоугольника из третьего столбца.
Найдём площадь прямоугольника из третьего столбца.
16
34
64
48
544
Пишу: 16•34.
Умножу первый множитель на число единиц: 16•4=64.
Получу первое неполное произведение: 64.
Умножу первый множитель на число десятков: 16•3=48.
Получу второе неполное произведение: 48 десятков.
Начну подписывать второе неполное произведение под десятками. Сложу неполные произведения.
Читаю ответ: 544. Это произведение чисел 16 и 34.
Значит, площадь прямоугольника из третьего столбца равна 544 дм2.
Найдём периметр прямоугольника из четвёртого столбца.
2•(25+25)=2•50=100 (дм) – периметр прямоугольника из четвёртого столбца.
Найдём площадь прямоугольника из четвёртого столбца.
25
25
125
50
625
Пишу: 25•25.
Умножу первый множитель на число единиц: 25•5=125.
Получу первое неполное произведение: 125.
Умножу первый множитель на число десятков: 25•2=50.
Получу второе неполное произведение: 50 десятков.
Начну подписывать второе неполное произведение под десятками. Сложу неполные произведения.
Читаю ответ: 625. Это произведение чисел 25 и 25.
Значит, площадь прямоугольника из четвёртого столбца равна 625 дм2.
Если сравнивать длину и ширину из второго и пятого столбцов, мы заметим, что они равны, только стоят в другом порядке. Но от этого результаты вычислений не изменятся, поэтому периметр и площадь в пятом столбце совпадают с периметром и площадью во втором столбце.
Найдём периметр прямоугольника из шестого столбца.
2•(44+6)=2•50=100 (дм) – периметр прямоугольника из шестого столбца.
Найдём площадь прямоугольника из шестого столбца.
44
6
264
Пишу: 44•6.
Умножаю единицы: 4•6=24. 24 ед. – это 2 дес. 4 ед.; пишу 4 под единицами, а 2 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 4•6=24, да ещё 2.
24+2=26. 26 дес. – это 2 сот. 6 дес.; пишу 6 под дес., а 2 сотни пишу под сотнями, так как других сотен для умножения нет.
Читаю ответ: 264.
Значит, площадь прямоугольника из шестого столбца равна 264 дм2.
Сравним результаты в третьей и четвёртой строках таблицы.
Периметры всех прямоугольников равны, а площади – разные.
Значит, площадь прямоугольника не зависит от его периметра.
Наибольшую площадь (625 дм2) имеет прямоугольник при длине и ширине 25 дм.
Прямоугольник с одинаковыми длиной и шириной называется квадратом.
8. Из Санкт-Петербурга в Москву выехали одновременно три автомобиля. Первый из них прибыл в Москву через 8 ч 45 мин, второй — на 2 ч 56 мин позднее первого, а третий — на 1 ч 48 мин раньше второго. Сколько времени был в пути третий автомобиль?
9. (Задача Л. Н. Толстого.) Продавец продаёт шапку, которая стоит 10 р. Подходит покупатель, меряет и согласен взять, но у него есть только банкнота в 25 р. Продавец отсылает своего помощника с этими деньгами к соседке разменять. Помощник прибегает и отдаёт продавцу 10 р. + 10 р. + 5 р. Продавец отдаёт шапку и сдачу 15 р. Через какое-то время приходит соседка, говорит, что полученная ею банкнота в 25 р. фальшивая, и требует вернуть ей её деньги. Ну что делать? Продавец возвращает ей деньги. На сколько рублей обманули продавца?
Похожие решебники
Популярные решебники 4 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.