Стр.66 Часть 1 ГДЗ Дорофеев Миракова 4 класс (Математика)
Решение #1





Решение #2









Рассмотрим вариант решения задания из учебника Дорофеев, Миракова, Бука 4 класс, Просвещение:
4. Сравни.
376 + 177 + 223 + 124 и 800 35 · 10 и 34 · 20
128 + 435 + 165 + 272 и 1 000 9 · 100 и 90 · 10
Для того, чтобы сравнить выражения, необходимо вычислить их значения.
Вспомним переместительное свойство сложения – от перестановки слагаемых сумма не меняется.
Переместительное свойство сложения лежит в основе приёма группировки слагаемых. Смысл этого приёма заключается в изменении расположения слагаемых в сумме для удобства вычислений. При этом изменение порядка действий обычно показывают с помощью скобок.
376+177+223+124 ? 800
Найдём значение выражения в левой части неравенства.
376+177+223+124=(376+124)+(177+223)=500+400=900
900 > 800, значит и 376+177+223+124 > 800
128+435+165+272 ? 1 000
Найдём значение выражения в левой части неравенства.
128+435+165+272=(128+272)+(435+165)=400+600=1 000
1 000=1 000, значит и 128+435+165+272= 1 000
35•10 ? 34•20
При умножении числа на 10 (или на 100) достаточно к этому числу приписать справа один ноль (или два нуля): 35•10=350
Для того, что умножить двузначное число на круглое, достаточно его умножить на число десятков и к полученному произведению приписать справа ноль.
34•20=34•(2•10)=(34•2)•10=68•10=680
350 < 680, значит и 35•10 < 34•20
9•100 ? 90•10
При умножении числа на 10 (или на 100) достаточно к этому числу приписать справа один ноль (или два нуля).
9•100=900
90•10=900
900=900, значит и 9•100= 90•10
5. Найди длину ломаной линии, состоящей из трёх звеньев, если длина первого звена 2 дм 7 см, а длина каждого следующего звена на 1 дм 2 см больше предыдущего.
6. Вычисли значения выражений.
(50 · 7 - 80) : 9 · 2 + 240 800 : 2 + 60 : 15 · 100
700 - (400 + 150 · 3) : 2 420 - 70 · 4 + 381 : 3
Действия в числовых выражениях выполняются в следующем порядке:
- действия, записанные в скобках;
- умножение и деление;
- сложение и вычитание.
(50•7-80) :9•2+240=(350-80) :9•2+240=270:9•2+240=30•2+240=60+240=300
350
80
270
Пишу (единицы под единицами, десятки под десятками):
350-80.
Вычитаем единицы: 0-0=0. Пишу 0 под единицами.
Вычитаем десятки: из 5 десятков нельзя вычесть 8 десятков, поэтому возьмём из 3 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 3). 10+5=15.
Вычтем: 15-8=7. Пишу 7 под десятками.
Было 3 сотни, но после того, как 1 сотню заняли при вычитании десятков, осталось 2 сотни. Спускаем в ответ 2 сотни.
Читаем ответ: 270.
700-(400+150•3) :2=700-(400+450) :2=700-850:2=700-425=275
850
2
8 425
5
4
10
10
0
Пишем: 850:2.
Первое неполное делимое – 8 сотен. Значит, в частном будет 3 цифры.
Делю сотни: разделю 8 на 2, получу 4 - столько сотен будет в частном.
Умножу 2 на 4, получу 8 – столько сотен разделили.
Вычту: 8-8=0 – сотни разделили все.
Делю десятки: разделю 5 на 2, получу 2 – столько десятков будет в частном.
Умножу 2 на 2, получу 4 – столько десятков разделили.
Вычту: 5-4=1 - столько десятков осталось разделить.
Делю единицы: 1 десяток 0 единиц – это 10 единиц.
Разделю 10 на 2, получу 5 - столько единиц будет в частном.
Умножу 2 на 5, получу 10 – столько единиц разделили.
Вычту: 10-10=0 - единицы разделили все.
Читаю ответ: 425.
700
425
275
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями): 700-425.
Вычитаем единицы: из 0 ед. нельзя вычесть 5 ед., занять из 0 дес. нельзя, поэтому возьмём из 7 сот. 1 сот., то есть 10 дес. (для того, чтобы не забыть, поставим точку над цифрой 7). Распределим 10 десятков, как 9 десятков и 10 единиц. 10+0=10.
Вычтем: 10-5=5. Пишу 5 под единицами.
Вычитаем десятки: было 0 десятков, но после того, как заняли 1 сотню при вычитании единиц, осталось 9 десятков.
Вычтем: 9-2=7. Пишу 7 под десятками.
Вычитаем сотни: было 7 сотен, но после того, как 1 сотню заняли при вычитании единиц, осталось 6 сотен.
Вычтем: 6-4=2. Пишем 2 под сотнями.
Читаем ответ: 275.
800:2+60:15•100=400+60:15•100=400+4•100=400+400=800
При умножении числа на 10 (или на 100) достаточно к этому числу приписать справа один ноль (или два нуля).
420-70•4+381:3=420-280+381:3=420-280+127=140+127=267
381
3
3 127
8
6
21
21
0
Пишем: 381:3.
Первое неполное делимое – 3 сотни. Значит, в частном будет 3 цифры.
Делю сотни: разделю 3 на 3, получу 1 - столько сотен будет в частном.
Умножу 3 на 1, получу 3 – столько сотен разделили.
Вычту: 3-3=0 – сотни разделили все.
Делю десятки: разделю 8 на 3, получу 2 – столько десятков будет в частном.
Умножу 3 на 2, получу 6 – столько десятков разделили.
Вычту: 8-6=2 - столько десятков осталось разделить.
Делю единицы: 2 десятка 1 единица – это 21 единица.
Разделю 21 на 3, получу 7 - столько единиц будет в частном.
Умножу 3 на 7, получу 21 – столько единиц разделили.
Вычту: 21-21=0 - единицы разделили все.
Читаю ответ: 127.
7. За 2 ч воробей может пролететь 78 км, а стрекоза — 60 км.
Объясни, что означают выражения.
78 : 2 60 : 2 78 : 2 - 60 : 2 78 - 60 (78 - 60) : 2
Скорость – это расстояние, пройденное в единицу времени.
Запишем краткое условие задачи.
Время Расстояние Скорость
Воробей 2 ч 78 км ? км/ч
Стрекоза 2 ч 60 км ? км/ч
Для того, чтобы найти скорость по известному расстоянию и времени, необходимо расстояние разделить на время.
78 – это расстояние, которое пролетел воробей, 2 – это время. Разделив расстояние на время, найдём скорость.
78:2 означает скорость воробья.
60 – это расстояние, которое пролетела стрекоза, 2 – это время. Разделив расстояние на время, найдём скорость.
60:2 означает скорость стрекозы.
Мы уже выяснили, что 78:2 - скорость воробья, а 60:2 - скорость стрекозы. Значит, их разность означает, на сколько воробей быстрее стрекозы.
78:2-60:2 означает, на сколько воробей быстрее стрекозы.
78 – расстояние, которое пролетел воробей за 2 часа, 60 – расстояние, которое пролетела стрекоза за 2 часа. Значит, их разность означает, на сколько больше пролетел воробей, чем стрекоза.
78-60 означает, на сколько больше пролетел воробей за 2 часа, чем стрекоза.
Мы уже выяснили, что 78-60 означает, на сколько больше пролетел воробей за 2 часа. Значит, если разность расстояний разделить ан время, то найдём разность скоростей – на сколько воробей быстрее стрекозы.
(78-60) :2 означает, на сколько воробей быстрее стрекозы.
8. Уроки в школе начинаются в 8 ч 30 мин. Каждый урок продолжается 45 мин. Перемены между вторым и третьим уроками, а также между третьим и четвёртым уроками длятся 20 мин. Продолжительность остальных перемен 10 мин. Определи время окончания пятого и шестого уроков.
Запишем краткое условие задачи.
Уроки начинаются - 8 ч 30 мин
Продолжительность урока - 45 мин
Перемены между 2-ым и 3-им, 3-им и 4-ым - 20 мин
Остальные перемены - 10 мин
Окончание пятого урока - ? ч
Окончание шестого урока - ? ч
Подумаем, как найти, сколько минут занимают уроки и перемены, и прибавить эту длительность к 8 ч 30 мин.
Каждый урок длится 45 минут. Значит, чтобы найти длительность 5 уроков, необходимо 45 умножить на 5.
45
5
225
Пишу: 45•5.
Умножаю единицы: 5•5=25. 25 ед. – это 2 дес. 5 единиц; пишу 5 под единицами, а 2 десятка запомню и прибавлю к десяткам.
Умножаю десятки: 4•5=20, да ещё 2.
20+2=22. 22 дес. – это 2 сот. 2 дес.; пишу 2 под дес., а 2 сотни пишу под сотнями, так как других сотен для умножения нет.
Читаю ответ: 225.
Значит, 5 уроков длятся 225 минут.
Между 5 уроками 4 перемены: 10 мин, 20 мин, 20 мин и 10 мин.
То есть две перемены по 10 мин и две перемены по 20 мин.
Умножим 10 на 2 и 20 на 2, сложим их и найдём, сколько минут занимают перемены между 5 уроками.
10•2=20
20•2=40
20+40=60
45•5+10•2+20•2=225+60=285 (мин) – занимают 5 уроков и перемены между ними.
Вспомним о том, что 1 ч=60 мин.
Переведём 285 минут в часы.
285 мин=240 мин+45 мин=4•60 мин+45 мин=
=4•1 ч+45 мин=4 ч+45 мин=4 ч 45 мин.
Найдём, во сколько закончится пятый урок.
8 ч 30 мин+4 ч 45 мин=(8 ч+30 мин)+(4 ч+45 мин)=8 ч+30 мин+4 ч+45 мин=(8 ч+4 ч)+(30 мин+45 мин)=12 ч+75 мин=12 ч+(60 мин+15 мин)=12 ч+(1 ч+15 мин)=12 ч+1 ч+15 мин=13 ч+15 мин=13 ч 15 мин - закончится пятый урок.
После пятого урока будет ещё одна перемена длиной 10 мин и урок длиной 45 мин. Прибавим их ко времени окончания пятого урока – 13 ч 15 мин.
13 ч 15 мин+10 мин+45 мин=13 ч+15 мин+10 мин+45 мин=13 ч+(15 мин+45 мин)+10 мин=13 ч+60 мин+10 мин=13 ч+1 ч+10мин=14 ч+10 мин=14 ч 10 мин - время окончания шестого урока.
Ответ: 13 ч 15 мин; 14 ч 10 мин.
9. Заполни пропуски в таблице, выполнив вычисления.
Объясни, почему периметр прямоугольника уменьшается на 10 м.
Периметр многоугольника – это сумма длин всех его сторон.
Противоположные стороны прямоугольника равны.
Для того, чтобы найти периметр, необходимо сложить все стороны. Длина и ширина прямоугольника – это две стороны. Для того, чтобы найти периметр, необходимо умножить сумму длины и ширины на 2, так как противоположные стороны прямоугольника равны.
Найдём периметр первого прямоугольника.
56+12=(50+6)+(10+2)=50+6+10+2=(50+10)+(6+2)=60+8=68
68•2=(60+8)•2=60•2+8•2=120+16=136
Мы знаем, что периметр – это удвоенная сумма длины и ширины. Значит, чтобы найти длину (ширину), необходимо периметр разделить на 2 и из результата вычесть ширину (длину).
Найдём длину второго прямоугольника.
126:2=(120+6):2=120:2+6:2=60+3=63
63-11=52 (м) – длина прямоугольника.
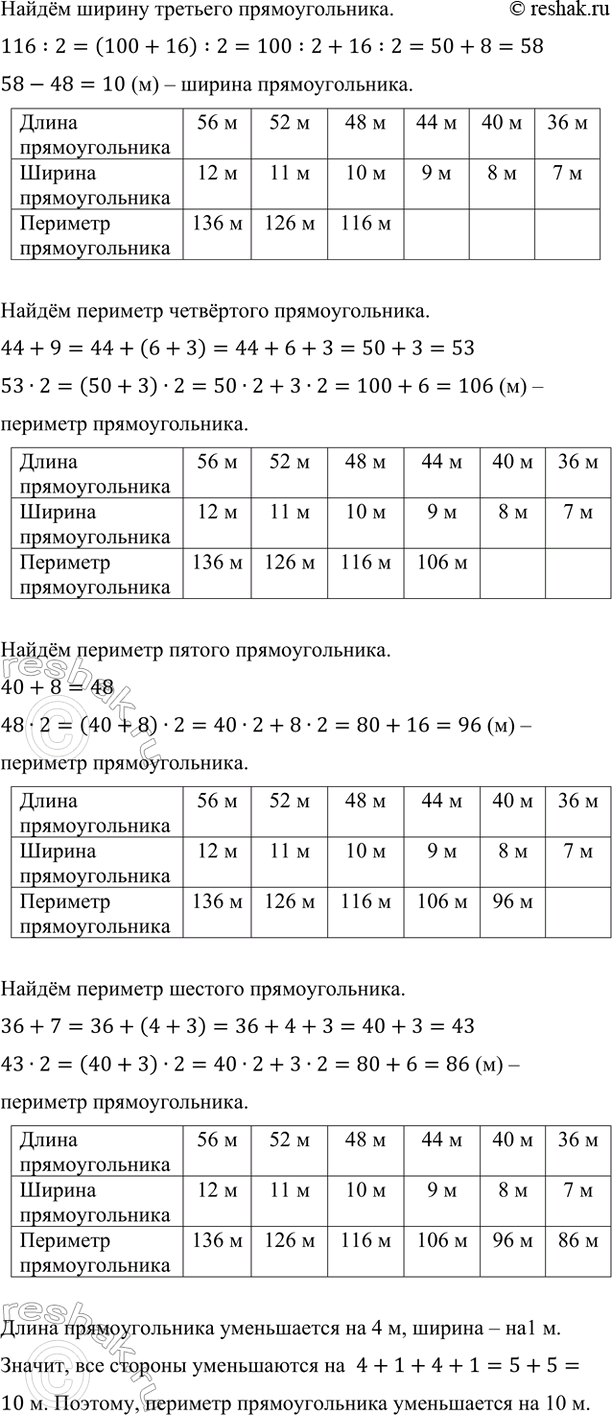
Найдём ширину третьего прямоугольника.
116:2=(100+16) :2=100:2+16:2=50+8=58
58-48=10 (м) – ширина прямоугольника.
Найдём периметр четвёртого прямоугольника.
44+9=44+(6+3)=44+6+3=50+3=53
53•2=(50+3)•2=50•2+3•2=100+6=106 (м) – периметр прямоугольника.
Найдём периметр пятого прямоугольника.
40+8=48
48•2=(40+8)•2=40•2+8•2=80+16=96 (м) – периметр прямоугольника.
Найдём периметр шестого прямоугольника.
36+7=36+(4+3)=36+4+3=40+3=43
43•2=(40+3)•2=40•2+3•2=80+6=86 (м) – периметр прямоугольника.
Длина прямоугольника уменьшается на 4 м, ширина – на1 м.
Значит, все стороны уменьшаются на 4+1+4+1=5+5=10 м. Поэтому, периметр прямоугольника уменьшается на 10 м.
10. В двух канистрах 28 л бензина. Если из первой канистры взять 3 л бензина, а во вторую добавить 2 л, то во второй канистре бензина будет на 7 л больше, чем останется в первой. Сколько литров бензина было первоначально в каждой канистре?
Запишем краткое условие задачи.
Было в 2-х канистрах - 28 л
Взяли из 1 канистры - 3 л
Добавили во 2 канистру - 2 л
Во 2 канистре - на 7 л больше, чем в 1
Было в каждой канистре первоначально - ? л
По условию задачи, из первой канистры взяли 3 л бензина, значит, общее количество (28 л) уменьшилось на 3 л.
Во вторую канистру добавили 2 л бензина, значит, общее количество увеличилось на 2 л.
Таким образом, из 28 л вычтем 3 л и прибавим 2 л.
28-3+2=25+2=27 (л) – бензина стало в двух канистрах.
Во второй канистре стало на 7 л больше, чем в первой.
Значит, если из второй канистры взять 7 л, то в ней станет столько же, сколько в первой канистре.
При этом общее количество тоже уменьшится на 7 л. Разделим его на 2 (так как в двух канистрах одинаковой количество бензина) и найдём, сколько бензина в первой канистре.
(27-7) :2=20:2=10 (л) – бензина стало в первой канистре.
Из первой канистры взяли 3 л бензина.
Значит, чтобы найти изначальное количество бензина, эти 3 л необходимо вернуть – к 10 л прибавить 3 л.
10+3=13 (л) – бензина было в первой канистре.
Изначально в двух канистрах было 28 л бензина, а в первой канистре было 13 л.
Значит, вычтем из 28 л 13 л и найдём, сколько бензина было во второй канистре изначально.
28-13=15 (л) – бензина было во второй канистре.
Ответ: 13 л и 15 л.
Похожие решебники
Популярные решебники 4 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.