Упр.506 Часть 1 ГДЗ Дорофеев Петерсон 5 класс (Математика)
Решение #1
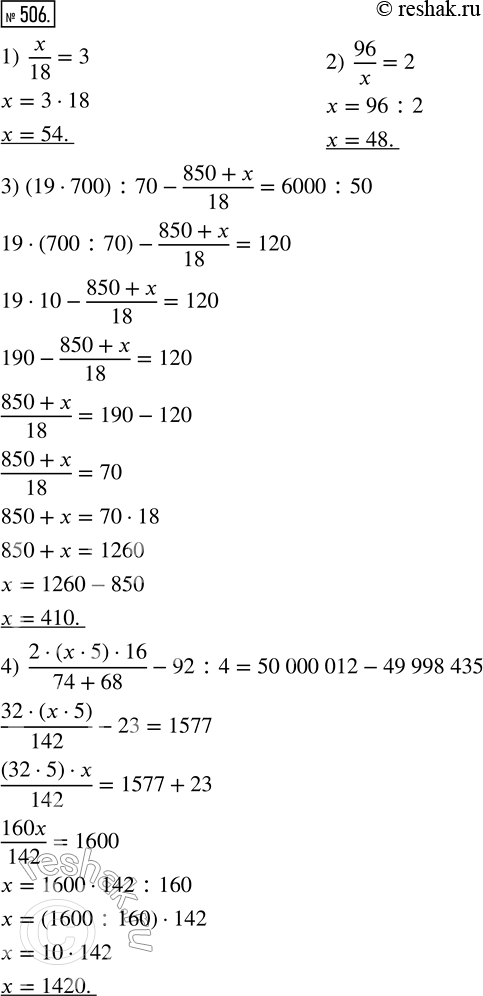
Решение #2







Рассмотрим вариант решения задания из учебника Дорофеев, Петерсон 5 класс, Бином:
506. Реши уравнение:
1) x/18 = 3; 3) (19 · 700) : 70 - (850 + x)/18 = 6000 : 50;
2) 96/x = 2; 4) (2 · (x · 5) · 16)/(74 + 68) - 92 : 4 = 50 000 012 - 49 998 435.
1) x/18=3
Черта обозначает деление. Тогда, в данном уравнении x – делимое, 18 – делитель, 3 – частное.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим x=3•18 или, выполнив умножение, x=3•(10+8)
x=3•10+3•8
x=30+24
x=54
2) 96/x=2
Черта обозначает деление. Тогда, в данном уравнении 96 – делимое, x – делитель, 2 – частное.
Для того, чтобы найти неизвестный делитель, необходимо делимое разделить на частное, получим x=96:2 или, выполнив деление, x=48.
96
2
8 48
16
16
0
Пишем: 96:2.
Первое неполное делимое – 9 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 9 на 2, получу 4 – столько десятков будет в частном.
Умножу 2 на 4, получу 8 – столько десятков разделили.
Вычту: 9-8=1 – столько десятков осталось разделить.
Делю единицы: 1 десяток 6 единиц – это 16 единиц.
Разделю 16 на 2, получу 8 – столько единиц будет в частном.
Умножу 2 на 8, получу 16 – столько единиц разделили.
Вычту: 16-16=0 – единицы разделили все.
Читаю ответ: 48.
3) (19•700) :70-(850+x)/18=6 000:50
Упростим выражение в левой части.
19•(700:70)-(850+x)/18=6 000:50
19•(700:70)-(850+x)/18=6 000:50
19•(70:7)-(850+x)/18=6 000:50
19•10-(850+x)/18=6 000:50
190-(850+x)/18=6 000:50
Упростим уравнение в левой части.
190-(850+x)/18=6 000:50
190-(850+x)/18=600:5
190-(850+x)/18=120
600
5
5 120
10
10
0
Пишем: 600:5.
Первое неполное делимое – 6 сотен. Значит, в частном будет 3 цифры.
Делю сотни: разделю 6 на 5, получу 1 – столько сотен будет в частном.
Умножу 5 на 1, получу 5 – столько сотен разделили.
Вычту: 6-5=1 – столько сотен осталось разделить.
Делю десятки: 1 сотня 0 десятков – это 10 десятков.
Разделю 10 на 5, получу 2 – столько десятков будет в частном.
Умножу 5 на 2, получу 10 – столько десятков разделили.
Вычту: 10-10=0 – десятки разделили все.
Осталось 0 единиц, поэтому пишем в частном 0, так как при делении 0 на любое число, получится 0.
Читаю ответ: 120.
В получившемся уравнении неизвестно вычитаемое (850+x)/18 .
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим (850+x)/18=190-120 или, выполнив вычитание, (850+x)/18=70.
Черта обозначает деление. Тогда, в данном уравнении 850+x – делимое, 18 – делитель, 70 – частное.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим 850+x=70•18
850+x=10•7•18
850+x=10•7•(10+8)
850+x=10•(7•10+7•8)
850+x=10•(70+56)
850+x=10•126
850+x=1 260
Неизвестно слагаемое x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим x=1 260-850 или, выполнив вычитание, x=410.
4) (2•(x•5)•16)/(74+68)-92:4=50 000 012-49 998 435
Упростим левую часть уравнения.
(2•(x•5)•16)/142-23=50 000 012-49 998 435
92
4
8 23
12
12
0
Пишем: 92:4.
Первое неполное делимое – 9 десятков. Значит, в частном будет 2 цифры.
Делю десятки: разделю 9 на 4, получу 2 – столько десятков будет в частном.
Умножу 4 на 2, получу 8 – столько десятков разделили.
Вычту: 9-8=1 – столько десятков осталось разделить.
Делю единицы: 1 десяток 2 единицы – это 12 единиц.
Разделю 12 на 4, получу 3 – столько единиц будет в частном.
Умножу 4 на 3, получу 12 – столько единиц разделили.
Вычту: 12-12=0 – единицы разделили все.
Читаю ответ: 23.
Упростим правую часть уравнения.
(2•(x•5)•16)/142-23=50 000 012-49 998 435
50 000 012
49 998 435
1 577
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч, единицы миллионов под единицами миллионов, десятки миллионов под десятками миллионов): 50 000 012-49 998 435.
Вычитаем единицы: из 2 единиц нельзя вычесть 5 единиц, поэтому возьмём из 1 десятка 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 1). 10+2=12.
Вычтем: 12-5=7. Пишу 7 под единицами.
Вычитаем десятки: был 1 дес., но после того, как при вычитании ед. заняли 1 дес., осталось 0 дес. Из 0 дес. нельзя вычесть 3 дес., занять из 0 сот., 0 ед. тыс., 0 дес. тыс., 0 сот. тыс., 0 ед. млн. нельзя, поэтому возьмём из 5 дес. млн. 1 дес. млн., то есть 10 ед. млн. (для того, чтобы не забыть, ставим точку над цифрой 5). Распределим 10 ед. млн., как 9 единиц миллионов, 9 сотен тысяч, 9 десятков тысяч, 9 единиц тысяч, 9 сотен и 10 десятков. 10+0=10.
Вычтем: 10-3=7. Пишем 7 под десятками.
Вычитаем сотни: было 0 сотен, но после того, как при вычитании десятков заняли 1 десяток миллионов, осталось 9 сотен.
Вычтем: 9-4=5. Пишем 5 под сотнями.
Вычитаем единицы тысяч: было 0 ед. тыс., но после того, как при вычитании дес. заняли 1 дес. миллионов, осталось 9 единиц тысяч.
Вычтем: 9-8=1. Пишем 1 под единицами тысяч.
Вычитаем десятки тысяч: было 0 дес. тыс., но после того, как при вычитании дес. заняли 1 дес. млн., осталось 9 десятков тысяч.
Вычтем: 9-9=0.
Вычитаем сотни тысяч: было 0 сот. тыс., но после того, как при вычитании дес. заняли 1 дес. миллионов, осталось 9 сотен тысяч.
Вычтем: 9-9=0.
Вычитаем единицы миллионов: было 0 ед. млн., но после того, как при вычитании дес. заняли 1 дес. млн., осталось 9 ед. миллионов.
Вычтем: 9-9=0.
Вычитаем десятки миллионов: было 5 дес. млн., но после того, как при вычитании дес. заняли 1 дес. млн., осталось 4 дес. миллионов.
Вычтем: 4-4=0.
0 под высшим разрядом принято не писать.
Читаем ответ: 1 577.
(2•(x•5)•16)/142-23=1 577
Решаем уравнение относительно вычитания, то есть неизвестно уменьшаемое (2•(x•5)•16)/142 .
Для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое, получим (2•(x•5)•16)/142=1 577+23 или, выполнив сложение, (2•(x•5)•16)/142=1 600.
Черта обозначает деление. Тогда, в данном уравнении
2•(x•5)•16 – делимое, 142 – делитель, 1 600 – частное.
Для того, чтобы найти неизвестное делимое, необходимо частное умножить на делитель, получим 2•(x•5)•16=1 600•142.
2•(x•5)•16=227 200
1 600•142 - это произведение 16 сотен и 142.
142
16
852
142
2272
Пишу: 142•16.
Умножу первый множитель на число единиц: 142•6=852.
Получу первое неполное произведение: 852.
Умножу первый множитель на число десятков: 142•1=142.
Получу второе неполное произведение: 142 десятка.
Начну подписывать второе неполное произведение под десятками. Сложу неполные произведения.
Припишу к произведению справа два нуля.
Читаю ответ: 227 200. Это произведение чисел 1 600 и 142.
Преобразуем левую часть уравнения.
2•(x•5)•16=227 200
2•x•5•16=227 200
10•16•x=227 200
160•x=227 200
Неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=227 200:160
x=227 200:160
x=22 720:16 или, выполнив деление, x=1 420.
22720
16
16
1420
67
64
32
32
0
Пишем: 22 720:16.
Первое неполное делимое – 22 тысячи. Значит, в частном будет 4 цифры.
Делю тысячи: разделю 22 на 16, получу 1 – столько тысяч будет в частном.
Умножу 16 на 1, получу 16 – столько тысяч разделили.
Вычту: 22-16=6 – столько тысяч осталось разделить.
Делю сотни: 6 тысяч 7 сотен – это 67 сотен.
Разделю 67 на 16, получу 4 – столько сотен будет в частном.
Умножу 16 на 4, получу 64 – столько сотен разделили.
Вычту: 67-64=3 – столько сотен осталось разделить.
Делю десятки: 3 сотни 2 десятка – это 32 десятка.
Разделю 32 на 16, получу 2 – столько десятков будет в частном.
Умножу 16 на 2, получу 32 – столько десятков разделили.
Вычту: 32-32=0 – десятки разделили все.
Осталось 0 единиц, поэтому пишем в частном 0, так как при делении 0 на любое число, получится 0.
Читаю ответ: 1 420.
Популярные решебники 5 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.





