Упр.32 Часть 1 ГДЗ Дорофеев Петерсон 5 класс (Математика)
Решение #1
Решение #2





Рассмотрим вариант решения задания из учебника Дорофеев, Петерсон 5 класс, Бином:
32. Верны ли неравенства:
а) 20 003 611 - 846 249 = < 12 307 579 + 6 849 604;
б) 9 352 796 + 20 647 204 > 7 000 000 - 1 949 495?
Для того, чтобы проверить верность неравенства, необходимо вычислить значения выражений в обеих частях неравенства.
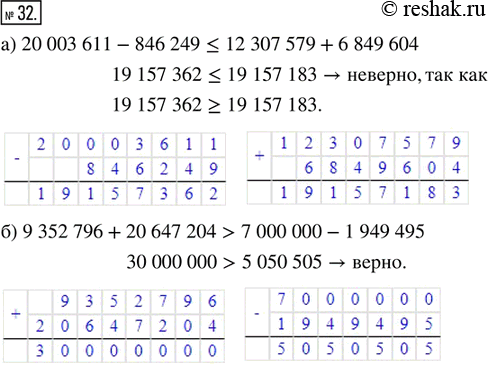
а) 20 003 611-846 249= < 12 307 579+6 849 604
Найдём значение выражения в левой части неравенства.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч):
20 003 611-846 249.
Вычитаем единицы: из 1 единицы нельзя вычесть 9 единиц, поэтому возьмём из 1 десятка 1 десяток, то есть 10 единиц (для того, чтобы не забыть, ставим точку над цифрой 2). 10+1=11.
Вычтем: 11-9=2. Пишу 2 под единицами.
Вычитаем десятки: был 1 дес., но после того, как при вычитании ед. заняли 1 дес., осталось 0 дес. Из 0 дес. нельзя вычесть 4 дес., поэтому возьмём из 6 сотен 1 сотню, то есть 10 десятков (для того, чтобы не забыть, ставим точку над цифрой 6). 10+0=10.
Вычтем: 10-4=6. Пишем 6 под десятками.
Вычитаем сотни: было 6 сотен, но после того, как 1 сотню заняли при вычитании десятков, осталось 5 сотен.
Вычтем: 5-2=3. Пишем 3 под сотнями.
Вычитаем единицы тысяч: из 3 ед. тыс. нельзя вычесть 6 ед. тыс., занять из 0 дес. тыс., 0 сот. тыс. и 0 ед. млн. нельзя, поэтому возьмём из 2 дес. млн. 1 десяток миллионов, то есть 10 единиц миллионов (для того, чтобы не забыть, ставим точку над цифрой 2). Распределим 10 единиц миллионов, как 9 единиц миллионов, 9 сотен тысяч, 9 десятков тысяч и 10 единиц тысяч. 10+3=13.
Вычтем: 13-6=7. Пишу 7 под единицами тысяч.
Вычитаем десятки тысяч: было 0 дес. тыс., но после того, как при вычитании ед. тыс. заняли 1 дес. млн., осталось 9 десятков тысяч.
Вычтем: 9-4=5. Пишем 5 под десятками тысяч.
Вычитаем сотни тысяч: было 0 сот. тыс., но после того, как при вычитании ед. тыс. заняли 1 дес. млн., осталось 9 сотен тысяч.
Вычтем: 9-8=1. Пишем 1 под сотнями тысяч.
Было 0 ед. млн., но после того, как при вычитании единиц тысяч заняли 1 десяток миллионов, осталось 9 единиц миллионов.
Было 2 дес. миллионов, но после того, как при вычитании единиц тысяч заняли 1 десяток миллионов, остался 1 десяток миллионов.
Читаем ответ: 19 157 362.
Найдём значение выражения в правой части неравенства.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч, единицы миллионов под единицами миллионов):
12 307 579+6 849 604.
Складываем единицы: 9+4=13. 13 ед. – это 1 дес. 3 ед.; пишу 3 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Складываем десятки: 7+0=7, да ещё 1.
7+1=8. Пишу 8 под десятками.
Складываем сотни: 5+6=11. 11 сот. – это 1 ед. тыс. 1 сот.; пишу 1 под сот., а 1 ед. тыс. запомню и прибавлю к ед. тысяч.
Складываем единицы тысяч: 7+9=16, да ещё 1.
16+1=17. 17 ед. тыс. – это 1 дес. тыс. 7 ед. тыс.; пишу 7 под ед. тыс., а 1 дес. тысяч запомню и прибавлю к десяткам тысяч.
Складываем десятки тысяч: 0+4=4, да ещё 1.
4+1=5. Пишу 5 под десятками тысяч.
Складываем сотни тысяч: 3+8=11. 11 сот. тыс. – это 1 ед. миллионов и 1 сотня тысяч; пишем 1 под сотнями тысяч, а 1 единицу миллионов запомню и прибавлю к единицам миллионов.
Складываем единицы миллионов: 2+6=8, да ещё 1.
8+1=9. Пишем 9 под единицами миллионов.
Спускаем в ответ 1 десяток миллионов.
Читаю ответ: 19 157 183.
Получилось неравенство 19 157 362= < 19 157 183 – неверно.
Так как в числах равное количество разрядов, то сравниваем поразрядно. Первые 5 разрядов чисел равны. Сравним шестые разряды: 3 > 1, значит, 19 157 362 > 19 157 183.
Значит, и исходное неравенство
20 003 611-846 249= < 12 307 579+6 849 604 – неверное.
б) 9 352 796+20 647 204 > 7 000 000-1 949 495
Найдём значение выражения в левой части неравенства.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч, единицы миллионов под единицами миллионов):
20 647 204+9 352 796.
Складываем единицы: 4+6=10. 10 ед. – это 1 дес. 0 ед.; пишу 0 под единицами, а 1 десяток запомню и прибавлю к десяткам.
Складываем десятки: 0+9=9, да ещё 1.
9+1=10. 10 десятков – это 1 сотня 0 десятков; пишу 0 под десятками, а 1 сотню запомню и прибавлю к сотням.
Складываем сотни: 2+7=9, да ещё 1.
9+1=10. 10 сот. – это 1 ед. тысяч 0 сотен; пишу 0 под сотнями, а 1 единицу тысяч запомню и прибавлю к единицам тысяч.
Складываем единицы тысяч: 7+2=9, да ещё 1.
9+1=10. 10 ед. тыс. – это 1 дес. тыс. 0 ед. тыс.; пишу 0 под ед. тысяч, а 1 десяток тысяч запомню и прибавлю к десяткам тысяч.
Складываем десятки тысяч: 4+5=9, да ещё 1.
9+1=10. 10 дес. тыс. – это 1 сот. тыс. 0 дес. тыс.; пишу 0 под дес. тысяч, а 1 сотню тысяч запомню и прибавлю к сотням тысяч.
Складываем сотни тысяч: 6+3=9, да ещё 1.
9+1=10. 10 сот. тыс. – это 1 ед. млн. и 0 сот. тыс.; пишем 0 под сот. тыс., а 1 ед. млн. запомню и прибавлю к ед. миллионов.
Складываем единицы миллионов: 0+9=9, да ещё 1.
9+1=10. 10 ед. млн. – это 1 дес. млн. 0 ед. млн.; пишем 0 под ед. млн., а 1 дес. млн. запомню и прибавлю к дес. миллионов.
Было 2 десятка миллионов, да ещё 1.
2+1=3. Пишем в ответ 3 десятка миллионов.
Читаю ответ: 30 000 000.
Найдём значение выражения в правой части неравенства.
Пишу (единицы под единицами, десятки под десятками, сотни под сотнями, единицы тысяч под единицами тысяч, десятки тысяч под десятками тысяч, сотни тысяч под сотнями тысяч, единицы миллионов под единицами миллионов):
7 000 000-1 949 495.
Вычитаем единицы: из 0 ед. нельзя вычесть 5 ед., занять из 0 дес., 0 сот., 0 ед. тыс., 0 дес. тыс., 0 сот. тыс. нельзя, поэтому возьмём из 7 единиц миллионов 1 единицу миллионов, то есть 10 сотен тысяч (для того, чтобы не забыть, ставим точку над цифрой 7). Распределим 10 сотен тысяч, как 9 сотен тысяч, 9 десятков тысяч, 9 единиц тысяч, 9 сотен, 9 десятков и 10 единиц. 10+0=10.
Вычтем: 10-5=5. Пишу 5 под единицами.
Вычитаем десятки: было 0 дес., но после того, как при вычитании единиц заняли 1 единицу миллионов, осталось 9 десятков.
Вычтем: 9-9=0. Пишем 0 под десятками.
Вычитаем сотни: было 0 сотен, но после того, как при вычитании единиц заняли 1 единицу миллионов, осталось 9 сотен.
Вычтем: 9-4=5. Пишем 5 под сотнями.
Вычитаем единицы тысяч: было 0 ед. тыс., но после того, как при вычитании ед. заняли 1 ед. миллионов, осталось 9 единиц тысяч.
Вычтем: 9-9=0. Пишу 0 под единицами тысяч.
Вычитаем десятки тысяч: было 0 дес. тыс., но после того, как при вычитании ед. заняли 1 ед. млн., осталось 9 десятков тысяч.
Вычтем: 9-4=5. Пишем 5 под десятками тысяч.
Вычитаем сотни тысяч: было 0 сот. тыс., но после того, как при вычитании ед. заняли 1 ед. миллионов, осталось 9 сотен тысяч.
Вычтем: 9-9=0. Пишем 0 под сотнями тысяч.
Вычитаем единицы миллионов: было 7 ед. млн., но после того, как при вычитании ед. заняли 1 ед. млн., осталось 6 ед. млн.
Вычтем: 6-1=5. Пишем 5 под единицами миллионов.
Читаем ответ: 5 050 505.
Получилось неравенство 30 000 000 > 5 050 505 – верно.
Так как в числе 30 000 000 большее количество разрядов, чем в числе 5 050 505
Значит, и исходное неравенство
9 352 796+20 647 204 > 7 000 000-1 949 495 – верное.
Популярные решебники 5 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.





