Упр.317 Часть 1 ГДЗ Дорофеев Петерсон 5 класс (Математика)
Решение #1
Решение #2


Рассмотрим вариант решения задания из учебника Дорофеев, Петерсон 5 класс, Бином:
317. Расположи карточки с числами и буквами в порядке возрастания чисел и зачеркни 3 буквы так, чтобы получилась фамилия известного русского художника.
Расположить карточки с числами в порядке возрастания, значит расположить их от самого меньшего к самому большему.
Вначале рассмотрим дроби, у которых нет целой части, так как они явно меньше дробей с целой частью.
Дробь 8/7=1 1/7 .
5/9,1/9,1/16,7/9,7/8
Приведём дроби к общему знаменателю 144.
5/9=(5•16)/(9•16)=80/144
1/9=(1•16)/(9•16)=16/144
1/16=(1•9)/(16•9)=9/144
7/9=(7•16)/(9•16)=112/144
7/8=(7•18)/(8•18)=126/144
Теперь расположим полученные дроби в порядке возрастания. Учтём, что среди дробей с равными знаменателями больше та дробь, числитель которой больше.
9/144,16/144,80/144,112/144,126/144
Таким образом, получим 1/16,1/9,5/9,7/9,7/8.
Остались дроби 1 3/7,1 5/6,1 1/7,1 5/7.
При сравнении дробей с одинаковыми знаменателями, больше та дробь, числитель которой больше.
Значит, 1 1/7,1 3/7,1 5/7
Сравним дроби 1 5/7 и 1 5/6.
При сравнении дробей с одинаковыми числителями, больше та дробь, знаменатель которой меньше.
Значит, 1 5/7 и 1 5/6
Получим 1/16,1/9,5/9,7/9,7/8,8/7,1 3/7,1 5/7,1 5/6,2
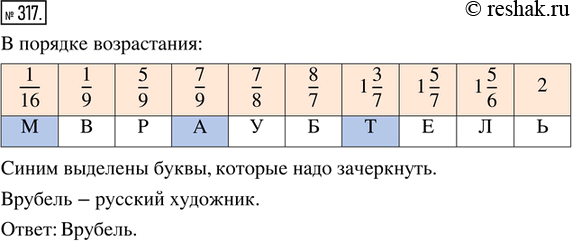
М, В, Р, А, У, Б, Т, Е, Л, Ь.
Зачеркнём 3 буквы, получим М, В, Р, А, У, Б, Т, Е, Л, Ь.
Врубель – фамилия известного русского художника.
Популярные решебники 5 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.





